
已知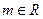 ,命题
,命题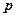 :对任意
:对任意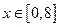 ,不等式
,不等式 恒成立;命题
恒成立;命题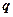 :存在
:存在 ,使不等式
,使不等式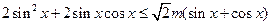 成立.
成立.
(1)若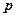 为真命题,求
为真命题,求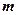 的取值范围;
的取值范围;
(2)若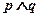 为假,
为假, 为真,求
为真,求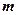 的取值范围。
的取值范围。
科目:高中数学 来源:2012-2013学年福建高二上学期第二次月考数学试卷 题型:解答题
已知 ,命题
,命题 :对任意
:对任意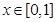 ,不等式
,不等式 恒成立;命题
恒成立;命题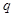 :存在
:存在 ,使得
,使得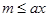 成立
成立
(Ⅰ)若 为真命题,求
为真命题,求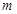 的取值范围;
的取值范围;
(Ⅱ)当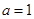 ,若
,若 且
且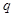 为假,
为假, 或
或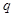 为真,求
为真,求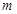 的取值范围。
的取值范围。
(Ⅲ)若 且
且 是
是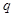 的充分不必要条件,求
的充分不必要条件,求 的取值范围。
的取值范围。
查看答案和解析>>
科目:高中数学 来源:2011-2012学年浙江省高三上学期期中考试文科数学试卷 题型:解答题
已知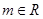 ,命题
,命题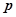 :对任意
:对任意 ,不等式
,不等式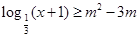 恒成立;命题
恒成立;命题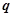 :存在
:存在 ,使不等式
,使不等式 成立.
成立.
(1)若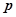 为真命题,求
为真命题,求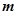 的取值范围;
的取值范围;
(2)若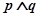 为假,
为假,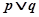 为真,求
为真,求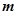 的取值范围。
的取值范围。
查看答案和解析>>
科目:高中数学 来源: 题型:
给出以下四个命题,所有真命题的序号为 。
①从总体中抽取的样本![]() ,则回归直线
,则回归直线![]() =
=![]() 必过点(
必过点(![]() )
)
②将函数![]() 的图象向右平移
的图象向右平移![]() 个单位,得到函数
个单位,得到函数![]() 的图象;
的图象;
③已知数列![]() ,那么“对任意的
,那么“对任意的![]() ,点
,点![]() 都在直线
都在直线![]() 上”是{
上”是{![]() }为等差数列的“充分不必要条件”
}为等差数列的“充分不必要条件”
④命题“若![]() ,则
,则![]() ”的否命题是“若
”的否命题是“若![]() ”
”
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com