【题目】2019年是中华人民共和国成立70周年，某校党支部举办了一场“我和我的祖国”知识竞赛，满分100分，回收40份答卷，成绩均落在区间
内，将成绩绘制成如下的频率分布直方图.
（1）估计知识竞赛成绩的中位数和平均数；
（2）从
，
分数段中，按分层抽样随机抽取5份答卷，再从对应的党员中选出3位党员参加县级交流会，求选出的3位党员中有2位成绩来自于分数段的概率.
【答案】（1）中位数为80.平均数为
（2）
【解析】
（1）由频率分布直方图可知，利用中位数和平均数的计算公式，即可求解.
（2）由频率分布直方图可知，分别求得
，
分数段中答卷数，利用列举法求得基本事件的总数，利用古典概型的概率计算公式，即可求解.
（1）由频率分布直方图可知，前3个小矩形的面积和为
，后2个小矩形的面积和为，所以估计中位数为80.
估计平均数为
.
（2）由频率分布直方图可知，分数段中答卷数分别为12，8，
抽取比例为
，所以，分数段中抽取的答卷数分别为3，2.
记中对应的3为党员为
，
，
，中对应的2为党员为
，
.
则从中选出对应的3位党员，共有不同的选法总数10种：
，
，
，
，
，
，
，
，
，
.
易知有2位来自于分数段的有3种，故所求概率为.
阅读快车系列答案科目：高中数学 来源： 题型：
【题目】下列命题中不正确的是（ ）
A. 平面
∥平面
，一条直线
平行于平面，则一定平行于平面
B. 平面∥平面，则内的任意一条直线都平行于平面
C. 一个三角形有两条边所在的直线分别平行于一个平面，那么该三角形所在的平面与这个平面平行
D. 分别在两个平行平面内的两条直线只能是平行直线或异面直线
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】数列{an}共有5项，其中a1=0，a5=2，且|ai+1﹣ai|=1，i=1，2，3，4，则满足条件的不同数列的个数为（ ）
A.3
B.4
C.5
D.6
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图为某旅游区各景点的分布图,图中一条带箭头的线段表示一段有方向的路,试计算顺着箭头方向,从A到H不同的旅游路线的条数,这个数是( )
A. 15 B. 16 C. 17 D. 18
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】(2015·陕西）如图，一横截面为等腰梯形的水渠，因泥沙沉积，导致水渠截面边界呈抛物线型（图中虚线表示），则原始的最大流量与当前最大流量的比值为 ．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某市出租车的计价标准是：4km以内（含4km）10元，超过4km且不超过18km的部分1.2元/km，超过18km的部分1.8元/km，不计等待时间的费用．
（1）如果某人乘车行驶了10km，他要付多少车费？
（2）试建立车费y（元）与行车里程x（km）的函数关系式．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某蔬菜基地种植西红柿，由历年市场行情得知，从二月一日起的300天内，西红柿市场销售价与上市时间的关系用图（1）的一条折线表示；西红柿的种植成本与上市时间的关系用图（2）的抛物线段表示.
（1）写出图（1）表示的市场售价与时间的函数关系式
写出图（2）表示的种植成本与时间的函数关系式
（2）认定市场售价减去种植成本为纯收益，问何时上市的西红柿收益最大？（注：市场售价和种植成本的单位：元/
kg，时间单位：天.）
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，在空间直角坐标系中有直三棱柱ABC﹣A1B1C1 ， CA=CC1=2CB，则直线BC1与直线AB1夹角的余弦值为（ ）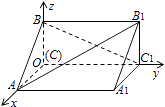
A.
B.
C.
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
