
【题目】如图,曲线C由上半椭圆 ![]() 和部分抛物线
和部分抛物线 ![]() 连接而成,C1与C2的公共点为A,B,其中C1的离心率为
连接而成,C1与C2的公共点为A,B,其中C1的离心率为 ![]() .
.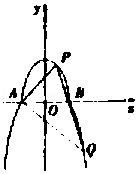
(1)求a,b的值;
(2)过点B的直线l与C1 , C2分别交于点P,Q(均异于点A,B),是否存在直线l,使得PQ为直径的圆恰好过点A,若存在直线l的方程;若不存在,请说明理由.
【答案】
(1)
解:在C1,C2的方程中,令y=0,可得b=1,且A(﹣1,0),B(1,0)是上半椭圆C1的左右顶点,
设C1的半焦距为c,由 ![]() 及a2﹣c2=b2﹣1,
及a2﹣c2=b2﹣1,
可得a=2,所以a=2,b=1
(2)
解:由(1),上半椭圆C1的方程为 ![]() ,
,
由题意知,直线l与x轴不重合也不垂直,设其方程为y=k(x﹣1)(k≠0),
代入C1的方程,整理得(k2+4)x2﹣2k2x+k2﹣4=0,
设点P的坐标为(xP,yP),
因为直线l过点B,所以x=1是方程的一个根,
由求根公式,得 ![]() ,所以点P的坐标为
,所以点P的坐标为 ![]() ,
,
同理,由 ![]() ,得点Q的坐标为(﹣k﹣1,﹣k2﹣2k),
,得点Q的坐标为(﹣k﹣1,﹣k2﹣2k),
所以 ![]() ,
,
依题意可知AP⊥AQ,所以 ![]() ,即
,即 ![]() ,
,
即 ![]() ,
,
因为k≠0,所以k﹣4(k+2)=0,解得 ![]() ,
,
经检验, ![]() 符合题意,故直线l的方程为
符合题意,故直线l的方程为 ![]()
【解析】(1)在C1 , C2的方程中,令y=0,可得b=1,且A(﹣1,0),B(1,0)是上半椭圆C1的左右顶点,设C1的半焦距为c,由 ![]() 及a2﹣c2=b2﹣1,联立解得a.(2)由(1),上半椭圆C1的方程为
及a2﹣c2=b2﹣1,联立解得a.(2)由(1),上半椭圆C1的方程为 ![]() ,由题意知,直线l与x轴不重合也不垂直,设其方程为
,由题意知,直线l与x轴不重合也不垂直,设其方程为
y=k(x﹣1)(k≠0),代入C1的方程,整理得(k2+4)x2﹣2k2x+k2﹣4=0,设点P的坐标为(xP , yP),由求根公式,得点P的坐标为 ![]() ,同理,由
,同理,由 ![]() ,得点Q的坐标为(﹣k﹣1,﹣k2﹣2k),依题意可知AP⊥AQ,所以
,得点Q的坐标为(﹣k﹣1,﹣k2﹣2k),依题意可知AP⊥AQ,所以 ![]() ,即可得出k.
,即可得出k.


 金钥匙试卷系列答案
金钥匙试卷系列答案科目:高中数学 来源: 题型:
【题目】设事件A表示“关于x的一元二次方程x2+ax+b2=0有实根”,其中a,b为实常数. (Ⅰ)若a为区间[0,5]上的整数值随机数,b为区间[0,2]上的整数值随机数,求事件A发生的概率;
(Ⅱ)若a为区间[0,5]上的均匀随机数,b为区间[0,2]上的均匀随机数,求事件A发生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】己知(2x﹣ ![]() )5(Ⅰ)求展开式中含
)5(Ⅰ)求展开式中含 ![]() 项的系数
项的系数
(Ⅱ)设(2x﹣ ![]() )5的展开式中前三项的二项式系数之和为M,(1+ax)6的展开式中各项系数之和为N,若4M=N,求实数a的值.
)5的展开式中前三项的二项式系数之和为M,(1+ax)6的展开式中各项系数之和为N,若4M=N,求实数a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】大学开设甲、乙、丙三门选修课供学生任意选修(也可不选),假设学生是否选修哪门课彼此互不影响.已知某学生只选修甲一门课的概率为0.08,选修甲和乙两门课的概率为0.12,至少选修一门的概率是0.88.
(1)求该学生选修甲、乙、丙的概率分别是多少?
(2)用ξ表示该学生选修的课程门数和没有选修的课程门数的乘积,求ξ的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆 ![]() 的左顶点和上顶点分别为A、B,左、右焦点分别是F1 , F2 , 在线段AB上有且只有一个点P满足PF1⊥PF2 , 则椭圆的离心率为( )
的左顶点和上顶点分别为A、B,左、右焦点分别是F1 , F2 , 在线段AB上有且只有一个点P满足PF1⊥PF2 , 则椭圆的离心率为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知实数λ>0,设函数f(x)=eλx﹣ ![]() .
.
(Ⅰ)当λ=1时,求函数g(x)=f(x)+lnx﹣x的极值;
(Ⅱ)若对任意x∈(0,+∞),不等式f(x)≥0恒成立,求λ的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 ![]() .
.
(1)求f(x)的最小正周期和单调递增区间;
(2)如果△ABC的三边a,b,c满足b2=ac,且边b所对角为x,试求x的范围及此时函数f(x)的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C所对的边分别为a,b,c,且asinAcosC+csinAcosA= ![]() c,D是AC的中点,且cosB=
c,D是AC的中点,且cosB= ![]() ,BD=
,BD= ![]() .
.
(1)求角A的大小;
(2)求△ABC的最短边的边长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com