
【题目】在△ABC中,内角A、B、C所对的边分别为a、b、c,已知a≠b,cos2A﹣cos2B= ![]() sinAcosA﹣
sinAcosA﹣ ![]() sinBcosB. (Ⅰ)求角C的大小;
sinBcosB. (Ⅰ)求角C的大小;
(Ⅱ)若c= ![]() ,siniA=
,siniA= ![]() ,求△ABC的面积.
,求△ABC的面积.
【答案】解:(Ⅰ)∵cos2A﹣cos2B= ![]() sinAcosA﹣
sinAcosA﹣ ![]() sinBcosB. ∴
sinBcosB. ∴ ![]() ﹣
﹣ ![]() =
= ![]() sin2A﹣
sin2A﹣ ![]() sin2B,…2分
sin2B,…2分
可得:cos2A﹣cos2B= ![]() sin2A﹣
sin2A﹣ ![]() sin2B,可得:sin(2A﹣
sin2B,可得:sin(2A﹣ ![]() )=sin(2B﹣
)=sin(2B﹣ ![]() ),…4分
),…4分
∵△ABC中,a≠b,可得A≠B,
∴2A﹣ ![]() +2B﹣
+2B﹣ ![]() =π,
=π,
∴A+B= ![]() ,可得:C=
,可得:C= ![]() …6分
…6分
(Ⅱ)由(Ⅰ)可得,A+B= ![]() ,
,
∵sinA= ![]() ,可得:A=
,可得:A= ![]() ,B=
,B= ![]() ,…8分
,…8分
∴sin ![]() =sin(
=sin( ![]() +
+ ![]() )=
)= ![]() ,…10分
,…10分
∵c= ![]() ,由正弦定理
,由正弦定理 ![]() ,可得:a=
,可得:a= ![]() ,…11分
,…11分
∴S△ABC= ![]() acsinB=
acsinB= ![]() …12分
…12分
(注:解法较多,酌情给分,直接sin ![]() =sin75°=
=sin75°= ![]() 的也给分)
的也给分)
【解析】(Ⅰ)利用三角函数恒等变换的应用化简已知等式可得sin(2A﹣ ![]() )=sin(2B﹣
)=sin(2B﹣ ![]() ),由A≠B,可得2A﹣
),由A≠B,可得2A﹣ ![]() +2B﹣
+2B﹣ ![]() =π,进而可求C的值.(Ⅱ)由(Ⅰ)可得,A+B=
=π,进而可求C的值.(Ⅱ)由(Ⅰ)可得,A+B= ![]() ,结合sinA=
,结合sinA= ![]() ,可得A,B的值,求得sin
,可得A,B的值,求得sin ![]() 的值,利用正弦定理可求a,进而利用三角形面积公式即可计算得解.
的值,利用正弦定理可求a,进而利用三角形面积公式即可计算得解.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】下列命题中正确的命题个数是( )
①. 如果![]() 共面,
共面, ![]() 也共面,则
也共面,则![]() 共面;
共面;
②.已知直线a的方向向量![]() 与平面
与平面![]() ,若
,若![]() //
// ![]() ,则直线a//
,则直线a// ![]() ;
;
③若![]() 共面,则存在唯一实数
共面,则存在唯一实数![]() 使
使![]() ,反之也成立;
,反之也成立;
④.对空间任意点O与不共线的三点A、B、C,若![]() =x
=x![]() +y
+y![]() +z
+z![]()
(其中x、y、z∈R),则P、A、B、C四点共面.
A. 3 B. 2 C. 1 D. 0
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】四棱锥P-ABCD中,AD⊥面PAB,BC⊥面PAB,底面ABCD为梯形,AD=4,BC=8,AB=6,∠APD=∠CPB,满足上述条件的四棱锥的顶点P的轨迹是( )
A. 圆的一部分 B. 椭圆的一部分
C. 球的一部分 D. 抛物线的一部分
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=log2(x+a).
(Ⅰ)当a=1时,若f(x)+f(x-1)>0成立,求x的取值范围;
(Ⅱ)若定义在R上奇函数g(x)满足g(x+2)=-g(x),且当0≤x≤1时,g(x)=f(x),求g(x)在[-3,-1]上的解析式,并写出g(x)在[-3,3]上的单调区间(不必证明);
(Ⅲ)对于(Ⅱ)中的g(x),若关于x的不等式g(![]() )≥g(-
)≥g(-![]() )在R上恒成立,求实数t的取值范围.
)在R上恒成立,求实数t的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业需要建造一个容积为8立方米,深度为2米的无盖长方体水池,已知池壁的造价为每平方米100元,池底造价为每平方米300元,设水池底面一边长为![]() 米,水池总造价为
米,水池总造价为![]() 元,求
元,求![]() 关于
关于![]() 的函数关系式,并求出水池的最低造价.
的函数关系式,并求出水池的最低造价.
查看答案和解析>>
科目:高中数学 来源: 题型:
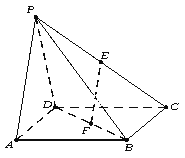
【题目】如图,在四棱锥P﹣ABCD中,底面ABCD是正方形,E、F分别为PC、BD的中点,侧面PAD⊥底面ABCD.
(1)求证:EF∥平面PAD;
(2)若EF⊥PC,求证:平面PAB⊥平面PCD.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了调查每天人们使用手机的时间,我校某课外兴趣小组在天府广场随机采访男性、女性用户各50 名,其中每天玩手机超过6小时的用户列为“手机控”,否则称其为“非手机控”,调查结果如下:
手机控 | 非手机控 | 合计 | |
男性 | 26 | 24 | 50 |
女性 | 30 | 20 | 50 |
合计 | 56 | 44 | 100 |
(1)根据以上数据,能否有60%的把握认为“手机控”与“性别”有关?
(2)现从调查的女性用户中按分层抽样的方法选出5人,求所抽取5人中“手机控”和“非手机控”的人数;
(3)从(2)中抽取的5人中再随机抽取3人,记这3人中“手机控”的人数为X,试求X的分布列与数学期望. 参考公式: ![]() .
.
参考数据:
P(K2≥k0) | 0.50 | 0.40 | 0.25 | 0.05 | 0.025 | 0.010 |
k0 | 0.456[ | 0.708 | 1.321 | 3.840 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,圆![]() 的方程为
的方程为![]() (
(![]() 为参数).以坐标原点为极点,
为参数).以坐标原点为极点,![]() 轴的正半轴为极轴,建立极坐标系,两种坐标系中取相同的单位长度,直线
轴的正半轴为极轴,建立极坐标系,两种坐标系中取相同的单位长度,直线![]() 的极坐标方程为
的极坐标方程为![]()
(1)当![]() 时,判断直线
时,判断直线![]() 与圆
与圆![]() 的关系;
的关系;
(2)当![]() 上有且只有一点到直线
上有且只有一点到直线![]() 的距离等于
的距离等于![]() 时,求
时,求![]() 上到直线
上到直线![]() 距离为
距离为![]() 的点的坐标.
的点的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
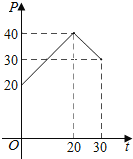
【题目】据市场调查发现,某种产品在投放市场的30天中,其销售价格![]() (元)和时间
(元)和时间![]() (天)的关系如图所示.
(天)的关系如图所示.
(1)求销售价格![]() (元)和时间
(元)和时间![]() (天)的函数关系式;
(天)的函数关系式;
(2)若日销售量![]() (件)与时间
(件)与时间![]() (天)的函数关系式是
(天)的函数关系式是![]()
![]() ,问该产品投放市场第几天时,日销售额
,问该产品投放市场第几天时,日销售额![]() (元)最高,且最高为多少元?
(元)最高,且最高为多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com