
(本小题12分)定义运算:
(1)若已知 ,解关于
,解关于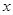 的不等式
的不等式
(2)若已知 ,对任意
,对任意 ,都有
,都有 ,求实数
,求实数 的取值范围。
的取值范围。
((1) ;(2)
;(2) .
.
【解析】
试题分析:(1)当 时,根据定义有
时,根据定义有

所以原不等式的解集为

(2)依题意知

因为对任意 ,都有
,都有 ,
,
所以
因为 的图像开口向下,对称轴为直线
的图像开口向下,对称轴为直线

①
若 ,即
,即 ,则
,则 在
在 为减函数,
为减函数,
所以 ,解得
,解得 ,所以
,所以

②
若 ,即
,即 ,则
,则 ,
,
解得 ,所以
,所以

③
若 ,即
,即 ,则
,则 在
在 为增函数,
为增函数,
所以 ,解得
,解得 ,所以
,所以

综上所述,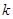 的取值范围是
的取值范围是

考点:本题主要以新定义为背景,考查恒成立问题.
点评:对于此类新定义问题,学生要注意仔细审题,冷静思考,新问题的解决还是要靠“老知识”“老方法”,应该有意识地运用转化思想,将新问题转化为我们熟知的问题。对于恒成立问题,要转为为求最值来解决,分情况讨论求最值时,要做到不重不漏.


科目:高中数学 来源:2015届陕西省高一上学期期中考试数学试卷(解析版) 题型:解答题
(本小题12分)已知函数 是定义在
是定义在 上的偶函数,已知
上的偶函数,已知 时,
时, .
.

(1)画出偶函数 的图象;
的图象;
(2)根据图象,写出 的单调区间;同时写出函数的值域.
的单调区间;同时写出函数的值域.
查看答案和解析>>
科目:高中数学 来源:2010年吉林省高二下学期期中考试数学(文) 题型:解答题
(本小题12分) 定义:若函数f(x)对于其定义域内的某一数x0,有f(x0)= x0,则称x0是f(x)的一个不动点.已知函数f(x)=ax2+(b+1)x+b-1(a≠0).
(1)当a=1,b=-2时,求函数f(x)的不动点;
(2)若对任意的实数b,函数f(x)恒有两个不动点,求a的取值范围;
(3)在(2)的条件下,若y=f(x)图象上两个点A、B的横坐标是函数f(x)的不动点,且A、B两点关于直线y=kx+ 对称,求b的最小值.
对称,求b的最小值.
查看答案和解析>>
科目:高中数学 来源:2010年河南省实验中学高二下学期期中考试数学(理) 题型:解答题
(本小题12分)定义在定义域D内的函数 ,若对任意的
,若对任意的 都有
都有 ,则称函数
,则称函数 为“妈祖函数”,否则称“非妈祖函数”.试问函数
为“妈祖函数”,否则称“非妈祖函数”.试问函数 ,
, )是否为“妈祖函数”?如果是,请给出证明;如果不是,请说明理由.
)是否为“妈祖函数”?如果是,请给出证明;如果不是,请说明理由.


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com