
【题目】在四棱锥 ![]() 中,
中, ![]() 平面
平面 ![]() ,
, ![]() ∥
∥ ![]() ,
, ![]() ,
,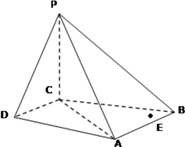
(1)求证: ![]() 平面
平面 ![]()
(2)求证:平面 ![]() 平面
平面 ![]()
(3)设点 ![]() 为
为 ![]() 中点,在棱
中点,在棱 ![]() 上是否存在点
上是否存在点 ![]() ,使得
,使得 ![]() ∥平面
∥平面 ![]() ?说明理由.
?说明理由.
科目:高中数学 来源: 题型:
【题目】给定两个命题p:函数y=x2+8ax+1在[﹣1,1]上单调递增;q:方程 ![]() =1表示双曲线,如果命题“p∧q”为假命题,“p∨q”为真命题,求实数a的取值范围.
=1表示双曲线,如果命题“p∧q”为假命题,“p∨q”为真命题,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】
(1)已知点M(1,-3),N(1,2),P(5,y),且∠NMP=90°,则log8(7+y)=.
(2)若把本题中“∠NMP=90°”改为“log8(7+y)= ![]() ”,其他条件不变,则∠NMP=.
”,其他条件不变,则∠NMP=.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l的倾斜角为135°,直线l1经过点A(3,2),B(a , -1),且l1与l垂直,直线l2:2x+by+1=0与直线l1平行,则a+b等于( )
A.-4
B.-2
C.0
D.2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P﹣ABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC,E是PC的中点.求证: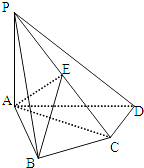
(Ⅰ)CD⊥AE;
(Ⅱ)PD⊥平面ABE.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知 ![]() 是单调递增的等差数列,首项
是单调递增的等差数列,首项 ![]() ,前
,前 ![]() 项和为
项和为 ![]() ,数列
,数列 ![]() 是等比数列,首项
是等比数列,首项 ![]() ,且
,且 ![]() .
.
(1)求数列 ![]() 和
和 ![]() 的通项公式;
的通项公式;
(2)设 ![]() ,求数列
,求数列 ![]() 的前
的前 ![]() 项和
项和 ![]() ;
;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,直四棱柱ABCD﹣A1B1C1D1中,AB∥CD,AD⊥AB,AB=2,AD= ![]() ,AA1=3,E为CD上一点,DE=1,EC=3
,AA1=3,E为CD上一点,DE=1,EC=3 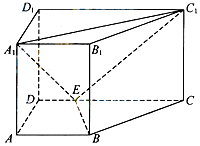
(1)证明:BE⊥平面BB1C1C;
(2)求三棱锥B1﹣EA1C1的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解少年儿童的肥胖是否与常喝碳酸饮料有关,现对100名六年级学生进行了问卷调查得到如图联表.且平均每天喝500ml以上为常喝,体重超过50kg为肥胖.已知在全部100人中随机抽取1人,抽到肥胖的学生的概率为0.8.
常喝 | 不常喝 | 合计 | |
肥胖 | 60 | ||
不肥胖 | 10 | ||
合计 | 100 |
(1)求肥胖学生的人数并将上面的列联表补充完整;
(2)是否有95%的把握认为肥胖与常喝碳酸饮料有关?说明你的理由. 附:参考公式:x2= ![]()
P(x2≥x0) | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
x0 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com