解:(1)由正弦定理得:

=

=

=2R,
∴a=2RsinA,b=2RsinB,c=2RsinC,
代入已知的等式得:
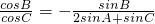
,
化简得:2sinAcosB+sinCcosB+cosCsinB
=2sinAcosB+sin(C+B)=2sinAcosB+sinA=sinA(2cosB+1)=0,
又A为三角形的内角,得出sinA≠0,
∴2cosB+1=0,即cosB=-

,
∵B为三角形的内角,∴
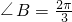
;
(2)∵a=4,sinB=

,S=5

,
∴S=

acsinB=

×4c×

=5

,
解得c=5,又cosB=-

,a=4,
根据余弦定理得:
b
2=a
2+c
2-2ac•cosB=16+25+20=61,
解得b=
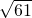
.
分析:(1)根据正弦定理化简已知的等式,然后再利用两角和与差的正弦函数公式及诱导公式变形,提取sinA,可得sinA与1+2sinB至少有一个为0,又A为三角形的内角,故sinA不可能为0,进而求出sinB的值,由B的范围,利用特殊角的三角函数值即可求出B的度数;
(2)由第一问求出的B的度数求出sinB和cosB的值,再由a的值及S的值,代入三角形的面积公式求出c的值,然后再由cosB的值,以及a与c的值,利用余弦定理即可求出b的值.
点评:此题考查了正弦、余弦定理,以及三角形的面积公式,考查了两角和与差的正弦函数公式及诱导公式,其中熟练掌握公式及定理,牢记特殊角的三角函数值是解本题的关键.

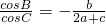
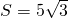 ,求b的值.
,求b的值. =
= =
= =2R,
=2R,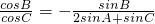 ,
, ,
,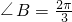 ;
; ,S=5
,S=5 ,
, acsinB=
acsinB= ×4c×
×4c× =5
=5 ,
, ,a=4,
,a=4,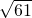 .
.

 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案