
【题目】如图,三棱锥A﹣BCD中,AB⊥平面BCD,CD⊥BD. 
(1)求证:CD⊥平面ABD;
(2)若AB=BD=CD=1,M为AD中点,求三棱锥A﹣MBC的体积.
【答案】
(1)证明:∵AB⊥平面BCD,CD平面BCD,
∴AB⊥CD,
∵CD⊥BD,AB∩BD=B,
∴CD⊥平面ABD;
(2)解:∵AB⊥平面BCD,BD平面BCD,
∴AB⊥BD.
∵AB=BD=1,
∴S△ABD= ![]() ,
,
∵M为AD中点,
∴S△ABM= ![]() S△ABD=
S△ABD= ![]() ,
,
∵CD⊥平面ABD,
∴VA﹣MBC=VC﹣ABM= ![]() S△ABMCD=
S△ABMCD= ![]()
【解析】(1)证明:CD⊥平面ABD,只需证明AB⊥CD;(2)利用转换底面,VA﹣MBC=VC﹣ABM= ![]() S△ABMCD,即可求出三棱锥A﹣MBC的体积.
S△ABMCD,即可求出三棱锥A﹣MBC的体积.
【考点精析】通过灵活运用直线与平面垂直的判定,掌握一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直;注意点:a)定理中的“两条相交直线”这一条件不可忽视;b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想即可以解答此题.


科目:高中数学 来源: 题型:
【题目】现有8名奥运会志愿者,其中志愿者A1 , A2 , A3通晓日语,B1 , B2 , B3通晓俄语,C1 , C2通晓韩语.从中选出通晓日语、俄语和韩语的志愿者各1名,组成一个小组.
(1)求A1被选中的概率;
(2)求B1和C1不全被选中的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC 中,角A,B,C所对的边分別为a,b,c,且asin Acos C+csin AcosA= ![]() c
c
(1)若c=1,sin C= ![]() ,求△ABC的面积S
,求△ABC的面积S
(2)若D 是AC的中点且cosB= ![]() ,BD=
,BD= ![]() ,求△ABC的最短边的边长.
,求△ABC的最短边的边长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设命题p:实数x满足x2﹣4ax+3a2<0,其中a>0,命题q:实数x满足 ![]() .
.
(1)若a=1,且p∧q为真,求实数x的取值范围;
(2)若p是q的充分不必要条件,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=sinωx+cosωx(ω>0),x∈R,若函数f(x)在区间(﹣ω,ω)内单调递增,且函数y=f(x)的图象关于直线x=ω对称,则ω的值为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=loga(2x+1),g(x)=loga(1﹣2x)(a>0且a≠1)
(1)求函数F(x)=f(x)﹣g(x)的定义域;
(2)判断F(x)=f(x)﹣g(x)的奇偶性,并说明理由;
(3)确定x为何值时,有f(x)﹣g(x)>0.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知ACDE是直角梯形,且ED∥AC,平面ACDE⊥平面ABC,∠BAC=∠ACD=90°,AB=AC=AE=2, ![]() ,P是BC的中点. (Ⅰ)求证:DP∥平面EAB;
,P是BC的中点. (Ⅰ)求证:DP∥平面EAB;
(Ⅱ)求平面EBD与平面ABC所成锐二面角大小的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某旅游城市为向游客介绍本地的气温情况,绘制了一年中各月平均最高气温和平均最低气温的雷达图,图中A点表示十月的平均最高气温约为15℃,B点表示四月的平均最低气温约为5℃,下面叙述不正确的是( ) 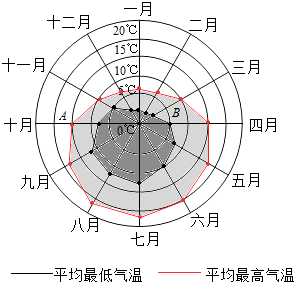
A.各月的平均最低气温都在0℃以上
B.七月的平均温差比一月的平均温差大
C.三月和十一月的平均最高气温基本相同
D.平均最高气温高于20℃的月份有5个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com