
【题目】已知圆M:(x+cos)2+(y-sin)2=1,直线l:y=kx,下面四个命题:
(A)对任意实数k与,直线l和圆M相切;
(B)对任意实数k与,直线l和圆M有公共点;
(C)对任意实数,必存在实数k,使得直线l与和圆M相切;
(D)对任意实数k,必存在实数,使得直线l与和圆M相切.
其中真命题的代号是______________(写出所有真命题的代号).
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】已知各项均不相等的等差数列{an}满足a1=1,且a1 , a2 , a5成等比数列.
(1)求{an}的通项公式;
(2)若bn=(﹣1)n ![]() (n∈N*),求数列{bn}的前n项和Sn .
(n∈N*),求数列{bn}的前n项和Sn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() (
(![]() )的左焦点为
)的左焦点为![]() ,左准线方程为
,左准线方程为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)已知直线![]() 交椭圆
交椭圆![]() 于
于![]() ,
, ![]() 两点.
两点.
①若直线![]() 经过椭圆
经过椭圆![]() 的左焦点
的左焦点![]() ,交
,交![]() 轴于点
轴于点![]() ,且满足
,且满足![]() ,
, ![]() .求证:
.求证: ![]() 为定值;
为定值;
②若![]() (
(![]() 为原点),求
为原点),求![]() 面积的取值范围.
面积的取值范围.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为选拔选手参加“中国汉字听写大全”,某中学举行了一次“汉字听写大赛”活动.为了了解本次竞赛学生的成绩情况,从中抽取了部分学生的分数作为样本(样本容量为n)进行统计.按照[50,60),[60,70),[70,80),[80,90),[90,100]的分组作出频率分布直方图,并作出样本分数的茎叶图(图中仅列出了得分在[50,60),[90,100]的数据). 
(Ⅰ)求样本容量n和频率分布直方图中的x、y的值;
(Ⅱ)在选取的样本中,从竞赛成绩在80分以上(含80分)的学生中随机抽取2名学生参加“中国汉字听写大会”,每次抽取1人,求在第1次抽取的成绩低于90分的前提下,第2次抽取的成绩仍低于90分的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一辆赛车在一个周长为![]() 的封闭跑道上行驶,跑道由几段直道和弯道组成,图
的封闭跑道上行驶,跑道由几段直道和弯道组成,图![]() 反映了赛车在“计时赛”整个第二圈的行驶速度与行驶路程之间的关系.
反映了赛车在“计时赛”整个第二圈的行驶速度与行驶路程之间的关系.

图1

图2
根据图![]() 有以下四个说法:
有以下四个说法:
①在这第二圈的![]() 到
到![]() 之间,赛车速度逐渐增加;
之间,赛车速度逐渐增加;
②在整个跑道中,最长的直线路程不超过![]() ;
;
③大约在这第二圈的![]() 到
到![]() 之间,赛车开始了那段最长直线路程的行驶;
之间,赛车开始了那段最长直线路程的行驶;
④在图![]() 的四条曲线(注:
的四条曲线(注:![]() 为初始记录数据位置)中,曲线
为初始记录数据位置)中,曲线![]() 最能符合赛车的运动轨迹.
最能符合赛车的运动轨迹.
其中,所有正确说法的序号是( )
A. ①②③ B. ②③ C. ①④ D. ③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某创业投资公司拟开发某种新能源产品,估计能获得![]() 万元到
万元到![]() 万元的投资利益,现准备制定一个对科研课题组的奖励方案:奖金
万元的投资利益,现准备制定一个对科研课题组的奖励方案:奖金![]() (单位:万元)随投资收益
(单位:万元)随投资收益![]() (单位:万元)的增加而增加,且奖金不超过
(单位:万元)的增加而增加,且奖金不超过![]() 万元,同时奖金不超过收益的
万元,同时奖金不超过收益的![]() .
.
(![]() )请分析函数
)请分析函数![]() 是否符合公司要求的奖励函数模型,并说明原因.
是否符合公司要求的奖励函数模型,并说明原因.
(![]() )若该公司采用函数模型
)若该公司采用函数模型![]() 作为奖励函数模型,试确定最小正整数
作为奖励函数模型,试确定最小正整数![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,边长为4的正方形![]() 与矩形
与矩形![]() 所在平面互相垂直,
所在平面互相垂直,![]() 分别为
分别为![]() 的中点,
的中点,![]() .
.

(1)求证:![]() 平面
平面![]() ;
;
(2)求证:![]() 平面
平面![]() ;
;
(3)在线段![]() 上是否存在一点
上是否存在一点![]() ,使得
,使得![]() ?若存在,求出
?若存在,求出![]() 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】公元263年左右,我国数学家刘徽发现,当圆内接多边形的边数无限增加时,多边形面积可无限逼近圆的面积,由此创立了割圆术,利用割圆术刘徽得到了圆周率精确到小数点后面两位的近似值3.14,这就是著名的徽率.如图是利用刘徽的割圆术设计的程序框图,则输出的n值为( ) 参考数据: ![]() ,sin15°≈0.2588,sin7.5°≈0.1305.
,sin15°≈0.2588,sin7.5°≈0.1305.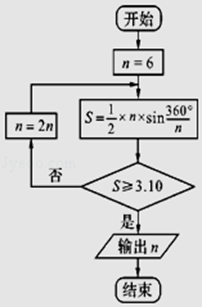
A.12
B.24
C.48
D.96
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com