
【题目】已知椭圆![]() 的离心率
的离心率![]() ,
,![]() 在椭圆上.
在椭圆上.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)已知动直线![]() (斜率存在)与椭圆相交于点
(斜率存在)与椭圆相交于点![]() 两点,且
两点,且![]() 的面积
的面积![]() ,若
,若![]() 为线段
为线段![]() 的中点.
的中点.![]() 点在
点在![]() 轴上投影为
轴上投影为![]() ,问:在
,问:在![]() 轴上是否存在两个定点
轴上是否存在两个定点![]() ,使得
,使得![]() 为定值,若存在求出
为定值,若存在求出![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
科目:高中数学 来源: 题型:
【题目】如图,为方便金湖县人民游览三河风景区附近的“网红桥”,现准备在河岸一侧建造一个观景台A,已知射线PM, PN为两边夹角为120°的公路(长度均超过5千米),在两条公路PM,PN上分别设立游客上下点B、C,在观景台A和游客上下点B、C之间和游客上下点B、C之间分别建造三条观光线路AB,AC,BC,测得PB=3干米,PC=5千米.

(1)求线段BC的长度;
(2)若∠BAC= 60°,因政府要计算修建三条观光线路所需费用,所以要计算AB,AC,BC三条线路的总长度的取值范围,请你建立合适的数学模型,帮助政府解决这个问题.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】了解某市今年初二年级男生的身体素质状况,从该市初二年级男生中抽取了一部分学生进行“掷实心球”的项目测试.成绩低于6米为不合格,成绩在6至8米(含6米不含8米)的为及格,成绩在8米至12米(含8米和12米,假定该市初二学生掷实心球均不超过12米)为优秀.把获得的所有数据,分成![]() 五组,画出的频率分布直方图如图所示.已知有4名学生的成绩在10米到12米之间.
五组,画出的频率分布直方图如图所示.已知有4名学生的成绩在10米到12米之间.
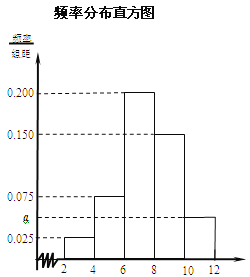
(Ⅰ)求实数![]() 的值及参加“掷实心球”项目测试的人数;
的值及参加“掷实心球”项目测试的人数;
(Ⅱ)根据此次测试成绩的结果,试估计从该市初二年级男生中任意选取一人,“掷实心球”成绩为优秀的概率;
(Ⅲ)若从此次测试成绩最好和最差的两组男生中随机抽取2 名学生再进行其它项目的测试,求所抽取的2名学生来自不同组的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校研究性学习小组对该校高三学生视力情况进行调查,在高三的全体1000名学生中随机抽取了100名学生的体检表,得到如图的频率分布直方图(图1).

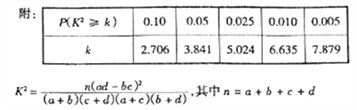
(1)若直方图中后四组的频数成等差数列,试估计全年级视力在5.0以下的人数;
(2)学习小组成员发现,学习成绩突出的学生,近视的比较多,为了研究学生的视力与学习成绩是否有关系,对年级名次在1~50名和951~1000名的学生进行了调查,得到图2中数据,根据表中的数据,能否在犯错误的概率不超过0.05的前提下认为视力与学习成绩有关系?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市创业园区新引进一家生产环保产品的公司,已知该环保产品每售出1盒的利润为0.3万元,当月未售出的环保产品,每盒亏损0.12万元.根据统计资料,该环保产品的市场月需求量的频率分布直方图如图所示.
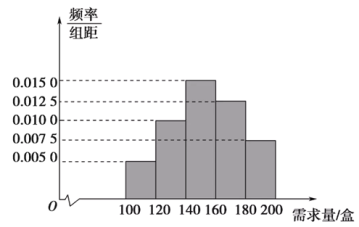
(1)若该环保产品的月进货量为160盒,以![]() (单位:盒,
(单位:盒,![]() )表示该产品一个月内的市场需求量,
)表示该产品一个月内的市场需求量,![]() (单位:万元)表示该公司生产该环保产品的月利润.
(单位:万元)表示该公司生产该环保产品的月利润.
①将![]() 表示为
表示为![]() 的函数;
的函数;
②根据频率分布直方图估计利润![]() 不少于39.6万元的概率.
不少于39.6万元的概率.
(2)在频率分布直方图的月需求量分组中,以各组的区间中点值代表该组的月需求量,当月进货量为158箱时,写出月利润![]() (单位:万元)的所有可能值.
(单位:万元)的所有可能值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(12分)已知函数f(x)=![]()
(1)判断函数在区间[1,+∞)上的单调性,并用定义证明你的结论.
(2)求该函数在区间[1,4]上的最大值与最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com