
【题目】设关于x的一元二次方程x2﹣2ax+b2=0.
(1)若a是从0、1、2、3四个数中任取的一个数,b是从0、1、2三个数中任取的一个数,求上述方程有实根的概率.
(2)若a是从区间[0,3]内任取的一个数,b是从区间[0,2]内任取的一个数,求上述方程有实根的概率.
【答案】
(1)解:∵关于x的一元二次方程x2﹣2ax+b2=0方程有实根,∴△=4a2﹣4b2≥0,
即a≥b
∵a是从0、1、2、3四个数中任取的一个数,b是从0、1、2三个数中任取的一个数,
∴转化为古典概率,
总的基本事件有4×3=12个,符合题意的有9个,
上述方程有实根的概率为 ![]() =
= ![]() .
.
(2)解:∵关于x的一元二次方程x2﹣2ax+b2=0,∴,△=4a2﹣4b2≥0,
即a≥b,且a∈[0,3],b∈[0,2],
建立几何概率:点(a,b),
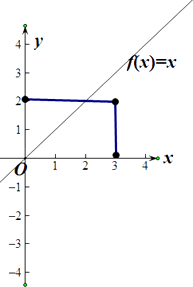
S的几何图形为矩形;面积为6,符合条件的图形Ω的面积为4,
方程有实根的概率为: ![]() .
.
【解析】(1)关于x的一元二次方程x2﹣2ax+b2=0,△=4a2﹣4b2≥0,转化为古典概率求解.(2)转化为几何概率求解.
【考点精析】通过灵活运用二次函数在闭区间上的最值,掌握当![]() 时,当
时,当![]() 时,
时,![]() ;当
;当![]() 时在
时在![]() 上递减,当
上递减,当![]() 时,
时,![]() 即可以解答此题.
即可以解答此题.


科目:高中数学 来源: 题型:
【题目】甲、乙两人参加某种选拔测试,在备选的10道题中,甲答对其中每道题的概率都是![]() ,乙能答对其中的5道题。规定每次考试都从备选的10道题中随机抽出3道题进行测试,答对一题加10分,答错一题(不答视为答错)减5分,至少得15分才能入选.
,乙能答对其中的5道题。规定每次考试都从备选的10道题中随机抽出3道题进行测试,答对一题加10分,答错一题(不答视为答错)减5分,至少得15分才能入选.
(I)求甲能入选的概率.
(II)求乙得分的分布列和数学期望;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知一组数据x1 , x2 , x3 , x4 , x5的平均数是2,方差是 ![]() ,那么另一组数据2x1﹣1,2x2﹣1,2x3﹣1,2x4﹣1,2x5﹣1的平均数,方差分别是( )
,那么另一组数据2x1﹣1,2x2﹣1,2x3﹣1,2x4﹣1,2x5﹣1的平均数,方差分别是( )
A.3, ![]()
B.3, ![]()
C.4, ![]()
D.4, ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,a、b、c分别是角A、B、C的对边,如果a,b,c成等差数列,B=60°,△ABC的面积为3 ![]() ,那么b等于( )
,那么b等于( )
A.2 ![]()
B.2 ![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了了解甲、乙两个工厂生产的轮胎的宽度是否达标,分别从两厂随机各选取了10个轮胎,将每个轮胎的宽度(单位:mm)记录下来并绘制出如下的折线图:
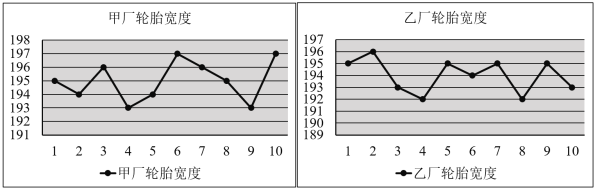
(1)分别计算甲、乙两厂提供的10个轮胎宽度的平均值;
(2)轮胎的宽度在![]() 内,则称这个轮胎是标准轮胎.试比较甲、乙两厂分别提供的10个轮胎中所有标准轮胎宽度的方差的大小,根据两厂的标准轮胎宽度的平均水平及其波动情况,判断这两个工厂哪个厂的轮胎相对更好?
内,则称这个轮胎是标准轮胎.试比较甲、乙两厂分别提供的10个轮胎中所有标准轮胎宽度的方差的大小,根据两厂的标准轮胎宽度的平均水平及其波动情况,判断这两个工厂哪个厂的轮胎相对更好?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在三棱锥P﹣ABC中,PA⊥平面ABC,AB=BC=AC=2,PA= ![]() ,E,F分别是PB,BC的中点,则EF与平面PAB所成的角等于( )
,E,F分别是PB,BC的中点,则EF与平面PAB所成的角等于( )
A.30°
B.45°
C.60°
D.90°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com