
【题目】如图,是一块半径为4米的圆形铁皮,现打算利用这块铁皮做一个圆柱形油桶.具体做法是从![]() 中剪裁出两块全等的圆形铁皮
中剪裁出两块全等的圆形铁皮![]() 与
与![]() 做圆柱的底面,剪裁出一个矩形
做圆柱的底面,剪裁出一个矩形![]() 做圆柱的侧面(接缝忽略不计),
做圆柱的侧面(接缝忽略不计),![]() 为圆柱的一条母线,点
为圆柱的一条母线,点![]() 在
在![]() 上,点
上,点![]() 在
在![]() 的一条直径上,
的一条直径上,![]() ,
,![]() 分别与直线
分别与直线![]() 、
、![]() 相切,都与
相切,都与![]() 内切.
内切.
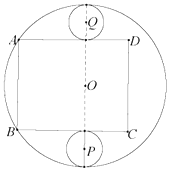
(1)求圆形铁皮![]() 半径的取值范围;
半径的取值范围;
(2)请确定圆形铁皮![]() 与
与![]() 半径的值,使得油桶的体积最大.(不取近似值)
半径的值,使得油桶的体积最大.(不取近似值)
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:高中数学 来源: 题型:
【题目】某高校进行自主招生测试,报考学生有500人,其中男生300人,女生200人,为了研究学生的成绩是否与性别有关,现采用分层抽样的方法,从中抽取了100名学生,先统计了他们测试的分数,然后按性别分为男、女两组,再将两组学生的分数分成4组:![]() ,
,![]() ,
,![]() ,
,![]() 分别加以统计,得到如图所示的频率分布直方图.
分别加以统计,得到如图所示的频率分布直方图.
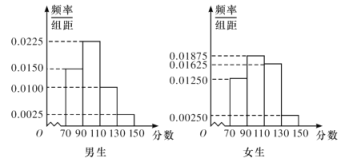
(Ⅰ)根据频率分布直方图可以估计女生测试成绩的平均值为103.5,请你估计男生测试成绩的平均值,由此推断男、女生测试成绩的平均水平的高低;
(Ⅱ)若规定分数不小于110分的学生为“优秀生”,请你根据已知条件完成![]() 列联表,并判断是否有
列联表,并判断是否有![]() 的把握认为“优秀生与性别有关”?
的把握认为“优秀生与性别有关”?
优秀生 | 非优秀生 | 合计 | |
男生 | |||
女生 | |||
合计 |
参考公式: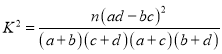 ,
,![]() .
.
参考数据:
P( | 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两班举行数学知识竞赛,参赛学生的竞赛得分统计结果如下表:
班级 | 参赛人数 | 平均数 | 中位数 | 众数 | 方差 |
甲 | 45 | 83 | 86 | 85 | 82 |
乙 | 45 | 83 | 84 | 85 | 133 |
某同学分析上表后得到如下结论:
①甲、乙两班学生的平均成绩相同;
②乙班优秀的人数少于甲班优秀的人数(竞赛得分![]() 分为优秀);
分为优秀);
③甲、乙两班成绩为85分的学生人数比成绩为其他值的学生人数多;
④乙班成绩波动比甲班小.
其中正确结论有( )
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆柱![]() 底面半径为1,高为
底面半径为1,高为![]() ,
,![]() 是圆柱的一个轴截面,动点
是圆柱的一个轴截面,动点![]() 从点
从点![]() 出发沿着圆柱的侧面到达点
出发沿着圆柱的侧面到达点![]() ,其距离最短时在侧面留下的曲线
,其距离最短时在侧面留下的曲线![]() 如图所示.将轴截面
如图所示.将轴截面![]() 绕着轴
绕着轴![]() 逆时针旋转
逆时针旋转![]() 后,边
后,边![]() 与曲线
与曲线![]() 相交于点
相交于点![]() .
.

(1)求曲线![]() 的长度;
的长度;
(2)当![]() 时,求点
时,求点![]() 到平面
到平面![]() 的距离.
的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 是抛物线
是抛物线![]() 上的两个点,点
上的两个点,点![]() 的坐标为
的坐标为![]() ,直线
,直线![]() 的斜率为
的斜率为![]() .设抛物线
.设抛物线![]() 的焦点在直线
的焦点在直线![]() 的下方.
的下方.
(Ⅰ)求k的取值范围;
(Ⅱ)设C为W上一点,且![]() ,过
,过![]() 两点分别作W的切线,记两切线的交点为
两点分别作W的切线,记两切线的交点为![]() . 判断四边形
. 判断四边形![]() 是否为梯形,并说明理由.
是否为梯形,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为 ,其中
,其中![]() 为参数,
为参数,![]() .在以坐标原点
.在以坐标原点![]() 为极点,轴的正半轴为极轴的极坐标系中,点
为极点,轴的正半轴为极轴的极坐标系中,点![]() 的极坐标为
的极坐标为![]() ,直线
,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的直角坐标方程与曲线
的直角坐标方程与曲线![]() 的普通方程;
的普通方程;
(2)若![]() 是曲线
是曲线![]() 上的动点,
上的动点,![]() 为线段
为线段![]() 的中点.求点
的中点.求点![]() 到直线
到直线![]() 的距离的最大值.
的距离的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在![]() 上的偶函数
上的偶函数![]() 满足
满足![]() ,且
,且![]() ,当
,当![]() 时,
时,![]() .已知方程
.已知方程![]() 在区间
在区间![]() 上所有的实数根之和为
上所有的实数根之和为![]() .将函数
.将函数![]() 的图象向右平移
的图象向右平移![]() 个单位长度,得到函数
个单位长度,得到函数![]() 的图象,则
的图象,则![]() __________,
__________,![]() __________.
__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)若函数f(x)的图象在点(2,f(2))处的切线方程为9x﹣y+b=0,求实数a,b的值;
(2)若a≤0,求f(x)的单调减区间;
(3)对一切实数a∈(0,1),求f(x)的极小值的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两人投篮命中的概率分别为![]() 与
与![]() ,各自相互独立.现两人做投篮游戏,共比赛3局,每局每人各投一球.
,各自相互独立.现两人做投篮游戏,共比赛3局,每局每人各投一球.
(1)求比赛结束后甲的进球数比乙的进球数多1的概率;
(2)设![]() 表示比赛结束后甲、乙两人进球数的差的绝对值,求
表示比赛结束后甲、乙两人进球数的差的绝对值,求![]() 的概率分布和数学期望
的概率分布和数学期望![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com