
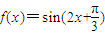 .
.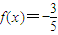 ,
,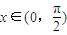 ,求sin2x的值.
,求sin2x的值.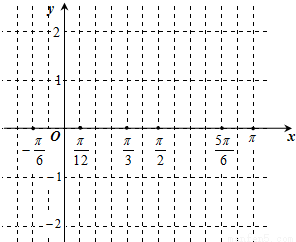
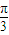 =0,
=0,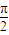 ,π,
,π,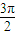 ,2π,求出对应的x即可找到五个特殊点的坐标,即可得到函数图象.
,2π,求出对应的x即可找到五个特殊点的坐标,即可得到函数图象.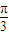 )的值,在利用两角差的余弦公式即可求出结论.
)的值,在利用两角差的余弦公式即可求出结论. =0,
=0,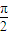 ,π,
,π, ,2π,
,2π, ,
, ,
, ,
, ,
, .
. 过点(-
过点(- ,0)(
,0)(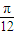 ,1),(
,1),(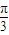 ,0),(
,0),( ,-1),(
,-1),( ,0).
,0). )的图象上各点的纵坐标不变,横坐标伸长到原来的2倍得到f(x)=sin(x+
)的图象上各点的纵坐标不变,横坐标伸长到原来的2倍得到f(x)=sin(x+ ),在整体相右平移
),在整体相右平移 个单位即可得到f(x)=sinx.
个单位即可得到f(x)=sinx. ),
), ∈(
∈( ,
, ),
),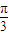 )=-
)=-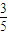 <0.
<0. )=-
)=- =-
=- .
. )-
)- ]
] )•cos
)•cos -cos(2x+
-cos(2x+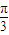 )•sin
)•sin
 )×
)× -(-
-(- )×
)×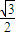
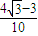 .
.

 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| -f(x) |
| 1 |
| f(x) |
查看答案和解析>>
科目:高中数学 来源: 题型:
| x2 |
| 4 |
| y2 |
| 3 |
| OP |
| FP |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:2010年浙江省高一上学期10月月考数学卷 题型:解答题
(本题10分)
已知函数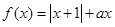 (
(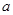 ∈R).
∈R).
(1)试给出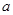 的一个值,并画出此时函数的图象;
的一个值,并画出此时函数的图象;
(2)若函数 f (x) 在 R 上具有单调性,求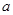 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com