解:(Ⅰ)∵f(x)=x
3+bx
2+cx,∴f'(x)=3x
2+2bx+c.…(1分)
∵F(x)=f(x)+af'(x)=x
3+(b+3a)x
2+(c+2ab)x+ac为奇函数,
由F(-x)=-F(x),可得b+3a=0,ac=0.
∵a>0,∴b=-3a,c=0.
∴
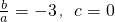
.…(3分)
(Ⅱ)由(Ⅰ)可得f(x)=x
3-3ax
2,
∴f'(x)=3x(x-2a).
令3x(x-2a)≤0,解得0≤x≤2a.
∴函数f(x)的单调递减区间为[0,2a]
(Ⅲ)当a=2时,曲线y=f(x)在点A(t,f(t))处的切线方程为:
y-f(t)=f'(t)(x-t),
k
AB=f'(t)=3t(t-4).
联立方程组
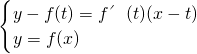
化简,得f(x)-f(t)=f'(t)(x-t).
即x
3-6x
2-t
3+6t
2=(3t
2-12t)(x-t),(x-t)(x
2+xt+t
2-6x-6t)=(x-t)(3t
2-12t).
∵A、B不重合,∴x≠t.
∴x
2+xt+t
2-6x-6t=3t
2-12t.
∴x
2+(t-6)x-2t
2+6t=0.
即(x-t)(x+2t-6)=0.
∵x≠t,∴x=-2t+6.
又另一交点为B(m,f(m)),∴m=-2t+6.…(2分)
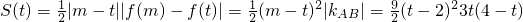
=
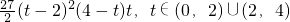
.
令h(t)=(t-2)
2(4-t)t,其中t∈(0,2)∪(2,4).
∵h(t)=-(t
4-8t
3+20t
2-16t),
∴h'(t)=-4(t
3-6t
2+10t-4)=
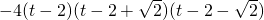
.
由
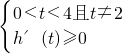
解得
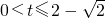
,或
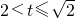
.
于是函数h(t)在区间(0,2
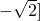
、(2,2+
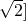
上是单调增函数;
在区间
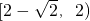
、
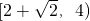
上是单调减函数.
当
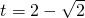
和
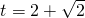
时,函数y=h(t)有极大值.
∴
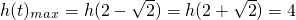
.
∴S(t)
max=54.…(3分)
分析:(Ⅰ) 利用两个向量平行的性质以及奇函数的定义,求出

和c的值;
(Ⅱ) 由导数小于0得到函数的减区间即可;
(Ⅲ) 利用曲线y=f(x)在点A(t,f(t))处的切线方程为y-f(t)=f′(x)(x-t),得(x-t)
2(x+2t-6)=0,则x=t或x=-2t+6,而A,B不重合,则m=-2t+6,S(t)=

|m-t|•|f(m)-f(t)|,=

t(t-2)
2(4-t),记k
PD =g(t),g′(t)=-

(3t-2)(t-2),利用g′(t)的符号列表求出g(t)的最值即得.
点评:本题考查两个向量平行的性质,函数的单调性与导数的关系,以及利用导数求函数的最大值、最小值等基础知识,考查运算求解能力,考查化归与转化思想.属于中档题.

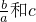 的值;
的值;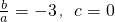 .…(3分)
.…(3分)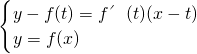
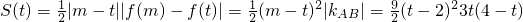 =
=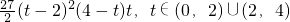 .
.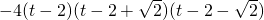 .
.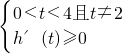
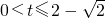 ,或
,或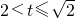 .
.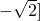 、(2,2+
、(2,2+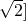 上是单调增函数;
上是单调增函数;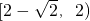 、
、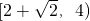 上是单调减函数.
上是单调减函数.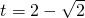 和
和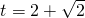 时,函数y=h(t)有极大值.
时,函数y=h(t)有极大值.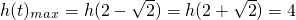 .
. 和c的值;
和c的值; |m-t|•|f(m)-f(t)|,=
|m-t|•|f(m)-f(t)|,= t(t-2)2(4-t),记kPD =g(t),g′(t)=-
t(t-2)2(4-t),记kPD =g(t),g′(t)=- (3t-2)(t-2),利用g′(t)的符号列表求出g(t)的最值即得.
(3t-2)(t-2),利用g′(t)的符号列表求出g(t)的最值即得.

 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案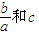 的值;
的值;