
【题目】已知函数![]() .
.
(1)求函数![]() 的单调区间;
的单调区间;
(2)若不等式![]() 时恒成立,求
时恒成立,求![]() 的取值范围.
的取值范围.
【答案】(1)见解析;(2)![]()
【解析】
(1)本题首先可以对函数![]() 进行求导,然后通过对
进行求导,然后通过对![]() 以及
以及![]() 两种情况进行分类讨论,分别求出每一种情况下函数
两种情况进行分类讨论,分别求出每一种情况下函数![]() 的单调性,即可得出结果;
的单调性,即可得出结果;
(2)本题首先可以将不等式![]() 在
在![]() 时恒成立转化为
时恒成立转化为![]() 在
在![]() 时恒成立,然后令
时恒成立,然后令![]() ,再对函数
,再对函数![]() 的导函数
的导函数![]() 的性质进行分类讨论,即可得出结果。
的性质进行分类讨论,即可得出结果。
(1)![]() ,
,
①若![]() ,
,![]() ,
,![]() 在
在![]() 上单调递增;
上单调递增;
②若![]() ,当
,当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,
,
所以![]() 是函数
是函数![]() 的单调递增区间,
的单调递增区间,![]() 是函数
是函数![]() 的单调减区间,
的单调减区间,
综上所述,当![]() 时,
时,![]() 的单调递增区间为
的单调递增区间为![]() ;
;
当![]() 时,
时,![]() 的单调递增区间为
的单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]() 。
。
(2)由题意可知,不等式可转化为![]() 在
在![]() 时恒成立,
时恒成立,
令![]() ,
,
![]() ,
,
①若![]() ,则
,则![]() ,
,![]() 在
在![]() 上单调递减,
上单调递减,
所以![]() ,不等式恒成立等价于
,不等式恒成立等价于![]() ,即
,即![]() ;
;
②若![]() ,则
,则![]() ,当
,当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,
,
![]() 在
在![]() 上单调递减,
上单调递减,![]() 在
在![]() 上单调递增,
上单调递增,
所以![]() ,不符合题意;
,不符合题意;
③若![]() ,当
,当![]() 时,
时,![]() ,
,![]() 在
在![]() 上单调递增,
上单调递增,
所以![]() ,不符合题意;
,不符合题意;
综上所述,![]() 。
。


科目:高中数学 来源: 题型:
【题目】如图,已知点![]() 是圆心为
是圆心为![]() 半径为
半径为![]() 的半圆弧上从点
的半圆弧上从点![]() 数起的第一个三等分点,点
数起的第一个三等分点,点![]() 是圆心为
是圆心为![]() 半径为
半径为![]() 的半圆弧的中点,
的半圆弧的中点,![]() 、
、![]() 分别是两个半圆的直径,
分别是两个半圆的直径,![]() ,直线
,直线![]() 与两个半圆所在的平面均垂直,直线
与两个半圆所在的平面均垂直,直线![]() 、
、![]() 共面.
共面.

(1)求三棱锥![]() 的体积;
的体积;
(2)求直线![]() 与
与![]() 所成角的余弦值.
所成角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》中有如下问题:今有蒲生一日,长三尺,莞生一日,长1尺.蒲生日自半,莞生日自倍.问几何日而长等?意思是:今有蒲第一天长高3尺,莞第一天长高1尺,以后蒲每天长高前一天的一半,莞每天长高前一天的2倍.若蒲、莞长度相等,则所需时间为()
(结果精确到0.1.参考数据:lg2=0.3010,lg3=0.4771.)
A.2.6天B.2.2天C.2.4天D.2.8天
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某电视台问政直播节目首场内容是“让交通更顺畅”.A、B、C、D四个管理部门的负责人接受问政,分别负责问政A、B、C、D四个管理部门的现场市民代表(每一名代表只参加一个部门的问政)人数的条形图如下.为了了解市民对武汉市实施“让交通更顺畅”几个月来的评价,对每位现场市民都进行了问卷调查,然后用分层抽样的方法从调查问卷中抽取20份进行统计,统计结果如下面表格所示:
满意 | 一般 | 不满意 | |
A部门 | 50% | 25% | 25% |
B部门 | 80% | 0 | 20% |
C部门 | 50% | 50% | 0 |
D部门 | 40% | 20% | 40% |

(1)若市民甲选择的是A部门,求甲的调查问卷被选中的概率;
(2)若想从调查问卷被选中且填写不满意的市民中再选出2人进行电视访谈,求这两人中至少有一人选择的是D部门的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点M在椭圆![]()
![]() 上,以M为圆心的圆与x轴相切于椭圆的右焦点F.
上,以M为圆心的圆与x轴相切于椭圆的右焦点F.
(Ⅰ)若圆M与y轴相切,求椭圆的离心率;
(Ⅱ)若圆M与y轴相交于A,B两点,且![]() 是边长为2的正三角形,求椭圆的方程.
是边长为2的正三角形,求椭圆的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列四种说法中:
①有两个面平行,其余各面都是平行四边形的几何体叫棱柱
②相等的线段在直观图中仍然相等
③一个直角三角形绕其一边旋转一周所形成的封闭图形叫圆锥
④用一个平面去截棱锥,底面与截面之间的部分组成的几何体叫棱台正确的个数是( )
A.0B.1C.2D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某单位鼓励员工参加健身运动,推广了一款手机软件,记录每人每天走路消耗的卡路里;软件的测评人员从员工中随机地选取了40人(男女各20人),记录他们某一天消耗的卡路里,并将数据整理如下:
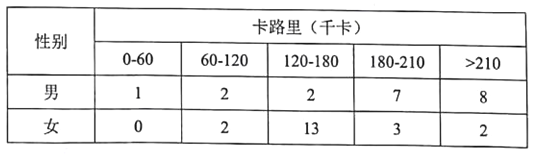
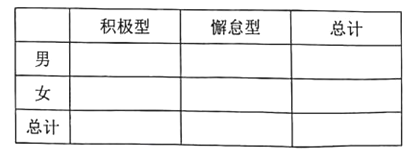
(1)已知某人一天的走路消耗卡路里超过180千卡被评测为“积极型”,否则为“懈怠型”,根据题中数据完成下面的![]() 列联表,并据此判断能否有99%以上把握认为“评定类型”与“性别”有关?
列联表,并据此判断能否有99%以上把握认为“评定类型”与“性别”有关?
(2)若测评人员以这40位员工每日走路所消耗的卡路里的频率分布来估计其所有员工每日走路消耗卡路里的频率分布,现在测评人员从所有员工中任选2人,其中每日走路消耗卡路里不超过120千卡的有![]() 人,超过210千卡的有
人,超过210千卡的有![]() 人,设
人,设![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
附: 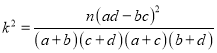 ,其中
,其中![]() .
.
参考数据:
| 0.10 | 0.05 | 0.025 | 0.010 |
| 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com