
| ˯��ʱ�䣨Сʱ�� | [4��5�� | [5��6�� | [6��7�� | [7��8�� | [8��9] |
| ���� | 2 | 4 | 8 | 4 | 2 |
| ˯��ʱ�䣨Сʱ�� | [4��5�� | [5��6�� | [6��7�� | [7��8�� | [8��9] |
| ���� | 1 | 5 | 6 | 5 | 3 |
| ˯��ʱ������7Сʱ | ˯��ʱ�䲻����7Сʱ | �ϼ� | |
| ���� | |||
| �� | |||
| �ϼ� |
| P��K2��k�� | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
���� ��1�������оٷ���������¼����Լ���Ӧ�¼��ĸ��ʣ�
��2����д2��2�����������ݹ�ʽ����۲�ֵ�����������ó�ͳ�ƽ��ۣ�
��� �⣺��1��ѡȡ��20��Ů���У���˯�����ز��㡱����2�ˣ���ΪA��B��
˯��ʱ����[5��6������4�ˣ���Ϊa��b��c��d��
����ѡȡ2�˵������AB��Aa��Ab��Ac��Ad��Ba��Bb��Bc��Bd��ab��ac��ad��bc��bd��cd��15�֣�
����ǡ��1�ˡ�˯�����ز��㡱����AB��Aa��Ab��Ac��Ad��Ba��Bb��Bc��Bd��8�֣�
���2����ǡ��һ��Ϊ������˯�߲��㡱�ĸ���ΪP=$\frac{8}{15}$��---6��
��2����д2��2���������£��������2�֣�
| ˯������7Сʱ | ˯�߲�����7Сʱ | �ϼ� | |
| ���� | 12 | 8 | 20 |
| �� | 14 | 6 | 20 |
| �ϼ� | 26 | 14 | 40 |
���� ���⿼�������оٷ���ŵ���͵ĸ������⣬Ҳ�����˶����Լ����Ӧ�����⣬�ǻ�����Ŀ��


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | P+R=2Q | B�� | Q��Q-P��=P��R-P�� | C�� | Q��Q-P��=R | D�� | Q2=PR |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
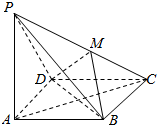 ��ͼ��������P-ABCD�У�PA�͵���ABCD���ҵ���ABCD�������Σ�DM��PC������ΪM��
��ͼ��������P-ABCD�У�PA�͵���ABCD���ҵ���ABCD�������Σ�DM��PC������ΪM���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
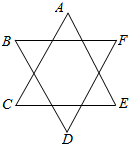 ��4�ֲ�ͬ����ɫ��ͼ��A��B��C��D��E��F���������Ⱦɫ��Ҫ��ͬһ�߶ε����㣨�磺AC��BD��������ɫ����ͬ���������ڵ����㣨�磺AB��BC��������ɫҲ����ͬ����ͬ��Ⱦɫ��������Ϊ96 ������ѧ���𣩣�
��4�ֲ�ͬ����ɫ��ͼ��A��B��C��D��E��F���������Ⱦɫ��Ҫ��ͬһ�߶ε����㣨�磺AC��BD��������ɫ����ͬ���������ڵ����㣨�磺AB��BC��������ɫҲ����ͬ����ͬ��Ⱦɫ��������Ϊ96 ������ѧ���𣩣��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
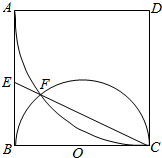 ��ͼ���ı���Ϊ�߳�Ϊa�������Σ���DΪԲ�ģ�DAΪ�뾶��Բ������BCΪֱ����ԲO����C��F������CF���ӳ���AB�ڵ�E��
��ͼ���ı���Ϊ�߳�Ϊa�������Σ���DΪԲ�ģ�DAΪ�뾶��Բ������BCΪֱ����ԲO����C��F������CF���ӳ���AB�ڵ�E���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | F��2 | B�� | F��2 | C�� | F��2 | D�� | F��2 |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com