
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 为正方形,
为正方形,![]() 底面
底面![]() ,
,![]() ,
,![]() 为线段
为线段![]() 的中点.
的中点.
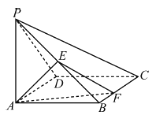
(1)若![]() 为线段
为线段![]() 上的动点,证明:平面
上的动点,证明:平面![]() 平面
平面![]() ;
;
(2)若![]() 为线段
为线段![]() ,
,![]() ,
,![]() 上的动点(不含
上的动点(不含![]() ,
,![]() ),
),![]() ,三棱锥
,三棱锥![]() 的体积是否存在最大值?如果存在,求出最大值;如果不存在,请说明理由.
的体积是否存在最大值?如果存在,求出最大值;如果不存在,请说明理由.
【答案】(1)证明见解析;(2)存在,![]() .
.
【解析】
(1)利用![]() ,可得
,可得![]() 平面
平面![]() ,根据面面垂直的判定定理可证平面
,根据面面垂直的判定定理可证平面![]() 平面
平面![]() ;
;
(2) 由![]() 底面
底面![]() ,得平面
,得平面![]() 平面
平面![]() .将问题转化为点
.将问题转化为点![]() 到直线
到直线![]() 的距离有无最大值即可解决.
的距离有无最大值即可解决.
(1)证明:因为![]() ,
,![]() 为线段
为线段![]() 的中点,所以
的中点,所以![]() ,
,
因为![]() 底面
底面![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() ,
,
又因为底面![]() 为正方形,所以
为正方形,所以![]() ,
,![]() ,
,
所以![]() 平面
平面![]() ,
,
因为![]() 平面
平面![]() ,所以
,所以![]() ,
,
因为![]() ,所以
,所以![]() 平面
平面![]() ,
,
因为![]() 平面
平面![]() ,所以平面
,所以平面![]() 平面
平面![]() .
.
(2)由![]() 底面
底面![]() ,则平面
,则平面![]() 平面
平面![]() ,
,
所以点![]() 到平面
到平面![]() 的距离(三棱锥
的距离(三棱锥![]() 的高)等于点
的高)等于点![]() 到直线
到直线![]() 的距离,
的距离,
因此,当点![]() 在线段
在线段![]() ,
,![]() 上运动时,三棱锥
上运动时,三棱锥![]() 的高小于或等于2,
的高小于或等于2,
当点![]() 在线段
在线段![]() 上运动时,三棱锥
上运动时,三棱锥![]() 的高为2,
的高为2,
因为![]() 的面积为
的面积为![]() ,
,
所以当点![]() 在线段
在线段![]() 上,三棱锥
上,三棱锥![]() 的体积取得最大值,
的体积取得最大值,
最大值为![]() .
.
由于三棱锥![]() 的体积等于三棱锥
的体积等于三棱锥![]() 的体积,
的体积,
所以三棱锥![]() 的体积存在最大值
的体积存在最大值![]() .
.


科目:高中数学 来源: 题型:
【题目】天干地支纪年法,源于中国,中国自古便有十天干与十二地支.十天干:甲、乙、丙、丁、戊、己、庚、辛、壬、癸.十二地支:子、丑、寅、卯、辰、巳、午、未、申、酉、戌、亥.天干地支纪年法是按顺序以一个天干和一个地支相配,排列起来,天干在前,地支在后,天干由“甲”起,地支由“子”起,比如第一年为“甲子”,第二年为“乙丑”,第三年为“丙寅”,…,以此类推,排列到“癸酉”后,天干回到“甲”重新开始,即“甲戌”,“乙亥”,之后地支回到“子”重新开始,即“丙子”,…,以此类推,已知2016年为丙申年,那么到改革开放100年时,即2078年为________年
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设m,n为平面α外两条直线,其在平面α内的射影分别是两条直线m1和n1,给出下列4个命题:①m1∥n1m∥n;②m∥nm1与n1平行或重合;③m1⊥n1m⊥n;④m⊥nm1⊥n1.其中所有假命题的序号是_____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)=6cos2![]() sinωx﹣3(ω>0)在一个周期内的图象如图所示,A为图象的最高点,B,C为图象与x轴的交点,且△ABC为正三角形
sinωx﹣3(ω>0)在一个周期内的图象如图所示,A为图象的最高点,B,C为图象与x轴的交点,且△ABC为正三角形
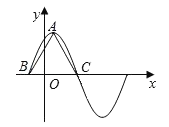
(1)求ω的值及函数f(x)的表达式;
(2)若f(x0)![]() ,且x0∈(
,且x0∈(![]() ),求f(x0+1)的值
),求f(x0+1)的值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】网购是现在比较流行的一种购物方式,现随机调查50名个人收入不同的消费者是否喜欢网购,调查结果表明:在喜欢网购的25人中有18人是低收入的人,另外7人是高收入的人,在不喜欢网购的25人中有6人是低收入的人,另外19人是高收入的人.
喜欢网购 | 不喜欢网购 | 总计 | |
低收入的人 | |||
高收入的人 | |||
总计 |
(Ⅰ)试根据以上数据完成![]() 列联表,并用独立性检验的思想,指出有多大把握认为是否喜欢网购与个人收入高低有关系;
列联表,并用独立性检验的思想,指出有多大把握认为是否喜欢网购与个人收入高低有关系;
(Ⅱ)将5名喜欢网购的消费者编号为1、2、3、4、5,将5名不喜欢网购的消费者编号也记作1、2、3、4、5,从这两组人中各任选一人进行交流,求被选出的2人的编号之和为2的倍数的概率.
参考公式:
参考数据:
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地要建造一个边长为2(单位:![]() )的正方形市民休闲公园
)的正方形市民休闲公园![]() ,将其中的区域
,将其中的区域![]() 开挖成一个池塘,如图建立平面直角坐标系后,点
开挖成一个池塘,如图建立平面直角坐标系后,点![]() 的坐标为
的坐标为![]() ,曲线
,曲线![]() 是函数
是函数![]() 图像的一部分,过边
图像的一部分,过边![]() 上一点
上一点![]() 在区域
在区域![]() 内作一次函数
内作一次函数![]() (
(![]() )的图像,与线段
)的图像,与线段![]() 交于点
交于点![]() (点
(点![]() 不与点
不与点![]() 重合),且线段
重合),且线段![]() 与曲线
与曲线![]() 有且只有一个公共点
有且只有一个公共点![]() ,四边形
,四边形![]() 为绿化风景区.
为绿化风景区.
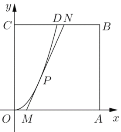
(1)求证:![]() ;
;
(2)设点![]() 的横坐标为
的横坐标为![]() ,
,
①用![]() 表示
表示![]() 、
、![]() 两点的坐标;
两点的坐标;
②将四边形![]() 的面积
的面积![]() 表示成关于
表示成关于![]() 的函数
的函数![]() ,并求
,并求![]() 的最大值.
的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com