【题目】地球海洋面积远远大于陆地面积，随着社会的发展，科技的进步，人类发现海洋不仅拥有巨大的经济利益，还拥有着深远的政治利益.联合国于第63届联合国大会上将每年的6月8日确定为“世界海洋日”.2019年6月8日，某大学的行政主管部门从该大学随机抽取100名大学生进行一次海洋知识测试，并按测试成绩（单位：分）分组如下：第一组[65，70），第二组[70，75），第二组[75，80），第四组[80，85），第五组[85，90]，得到频率分布直方图如下图：
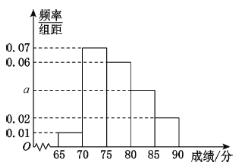
（1）求实数
的值；
（2）若从第四组、第五组的学生中按组用分层抽样的方法抽取6名学生组成中国海洋实地考察小队，出发前，用简单随机抽样方法从6人中抽取2人作为正、副队长，列举出所有的基本事件并求“抽取的2人为不同组”的概率.
【答案】（1）
（2）基本事件见解析, 所求的概率为
【解析】
（1）由所有小矩形面积和为1计算出
；
（2）先计算出第4、5两组人数，再按比例计算出抽取的人数，然后把第四组的4人表示为，
，
，
，第五组的2人表示为
，
，用列举法写出所有基本事件，并计数求出概率。
（1）据题意，得
，
∴.
（2）据题意知，随机抽取100名大学生中第四组有20人，
第五组有10人，
∴抽取6名学生中有第四组
人，即4人，
抽取6名学生中有第五组
人，即2人.
设6人中来自第四组的4人为，，，，来自第五组的2人为，，从中抽取2人的所有基本事件有：
，
，
，
，
，
，
，
，
，
，
，
，
，
，
共15种，
其中2人来自不同组的事件有，，，，，，，共8种，
∴所求的概率
.
科目：高中数学 来源： 题型：
【题目】某品牌餐饮公司准备在10个规模相当的地区开设加盟店，为合理安排各地区加盟店的个数，先在其中5个地区试点，得到试点地区加盟店个数分别为1，2，3，4，5时，单店日平均营业额
（万元）的数据如下：
加盟店个数 | 1 | 2 | 3 | 4 | 5 |
单店日平均营业额 | 10.9 | 10.2 | 9 | 7.8 | 7.1 |
（1）求单店日平均营业额（万元）与所在地区加盟店个数
（个）的线性回归方程；
（2）根据试点调研结果，为保证规模和效益，在其他5个地区，该公司要求同一地区所有加盟店的日平均营业额预计值总和不低于35万元，求一个地区开设加盟店个数
的所有可能取值；
（3）小赵与小王都准备加入该公司的加盟店，根据公司规定，他们只能分别从其他五个地区（加盟店都不少于2个）中随机选一个地区加入，求他们选取的地区相同的概率.
（参考数据及公式：
，
，线性回归方程
，其中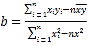
，
.）
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知直线
经过椭圆
的右焦点
，交椭圆
于点
，
，点
为椭圆的左焦点，
的周长为
..
（Ⅰ）求椭圆的标准方程；
（Ⅱ）若直线
与直线的倾斜角互补，且交椭圆于点
、
，
，求证：直线与直线的交点
在定直线上.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】《九章算术》中，将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马；将四个面都为直角三角形的三棱锥称之为鳖臑。若三棱锥P-ABC为鳖臑，PA⊥面ABC,PA=AB=2,AC=4,三棱锥P-ABC的四个顶点都在球的球面上，则球0的表面积为( )
A. 8πB. 12πC. 20πD. 24π
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，在四棱锥
中，
平面
，且
，
，
，点G，H分别为边
，
的中点，点M是线段
上的动点.
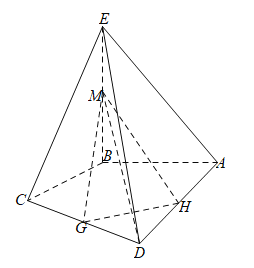
（1）求证：
；
（2）若
，当三棱锥
的体积最大时，求点C到平面
的距离.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数
，若曲线
在点
处的切线方程是
，不等式
的解集为非空集合
，其中
为自然对数的底数.
（Ⅰ）求的解析式，并用
表示
；
（Ⅱ）若任意
，不等式
恒成立，求实数的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
