
分析 (1)根据对数函数的性质求出函数的定义域即可;
(2)根据函数奇偶性的定义判断即可;
(3)令μ=2-ax,根据复合函数的单调性求出函数的最大值,从而求出对应的a的值即可.
解答 解:(1)由题意:f(x)=loga(2-3x),
∴2-3x>0,即x<$\frac{2}{3}$,
所以函数f(x)的定义域为(-∞,$\frac{2}{3}$);
(2)易知g(x)=loga(2-ax)-loga(2+ax),
∵2-ax>0且2+ax>0,
∴$-\frac{2}{a}<x<\frac{2}{a}$关于原点对称,
又∵$g(x)={log_a}(2-ax)-{log_a}(2+ax)={log_a}\frac{2-ax}{2+ax}$,
∴$g(-x)={log_a}\frac{2+ax}{2-ax}=-{log_a}\frac{2-ax}{2+ax}=-g(x)$,
∴g(x)为奇函数.
(3)令μ=2-ax,∵a>0,a≠1,
∴μ=2-ax在[2,3]上单调递减,
又∵函数f(x)在[2,3]递增,
∴0<a<1,又∵函数f(x)在[2,3]的最大值为1,
∴f(3)=1,即f(3)=loga(2-3a)=1,
∴$a=\frac{1}{2}$,∵0<a<1,∴$a=\frac{1}{2}$符合题意.
即存在实数$a=\frac{1}{2}$,使函数f(x)在[2,3]递增,并且最大值为1.
点评 本题考查了对数函数的性质,考查复合函数的单调性、最值问题,是一道中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
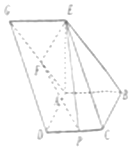 如图,已知四边形ABCD和ABEG均为平行四边形,点E在平面ABCD内的射影恰好为点A,以BD为直径的圆经过点A,C,AG的中点为F,CD的中点为P,且AD=AB=AE=2.
如图,已知四边形ABCD和ABEG均为平行四边形,点E在平面ABCD内的射影恰好为点A,以BD为直径的圆经过点A,C,AG的中点为F,CD的中点为P,且AD=AB=AE=2.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{9}$ | B. | $\frac{1}{6}$ | C. | $\frac{1}{3}$ | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | 02 | B. | 13 | C. | 42 | D. | 44 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-3,1] | B. | (-∞,1] | C. | [1,3) | D. | (3,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | 2 | C. | 1 | D. | 0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com