
(本题满分14分)数列![]() 满足
满足![]()
![]() .
.
(1)求数列{![]() }的通项公式;(2)设数列{
}的通项公式;(2)设数列{![]() }的前
}的前![]() 项和为
项和为![]() ,证明
,证明![]() .
.
科目:高中数学 来源: 题型:
(本题满分14分)学校为了了解高一新生男生的体能状况,从高一新生中抽取若干名男生进行铅球测试,把所得数据(精确到0.1米)进行整理后,分成6组画出频率分布直方图的一部分(如下图),已知从左到右前5个小组的频率分别为0.04,0.10,0.14,0.28,0.30. 第6小组的频数是7.
(1)请将频率分布直方图补充完整;
(2)该校参加这次铅球测试的男生有多少人?
(3)若成绩在8.0米以上(含8.0米)的为合格,试求这次铅球测试的成绩的合格率;
(4)在这次测试中,你能确定该校参加测试的男生铅球成绩的众数和中位数各落在哪个小组内吗?

查看答案和解析>>
科目:高中数学 来源:2011-2012学年广东省广州市高三上学期第3次月考理科数学试卷(解析版) 题型:解答题
把正奇数数列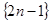 中的数按上小下大、左小右大的原则排成如下三角形数表:
中的数按上小下大、左小右大的原则排成如下三角形数表:
1
3 5
7 9 11
………………………
……………………………
设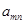
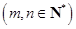 是位于这个三角形数表中从上往下数第
是位于这个三角形数表中从上往下数第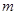 行、从左往右数第
行、从左往右数第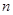 个数.
个数.
(1)若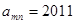 ,求
,求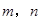 的值;
的值;
(2)若记三角形数表中从上往下数第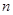 行各数的和为
行各数的和为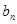 ,求证
,求证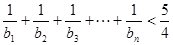 .(本题满分14分)
.(本题满分14分)
查看答案和解析>>
科目:高中数学 来源:2011-2012学年上海市闵行区高三上学期期末质量抽测理科数学试卷 题型:解答题
(本题满分14分)本题共有2个小题,第(1)小题满分6分,第(2)小题满分8分.
某地政府为改善居民的住房条件,集中建设一批经适楼房.用了1400万元购买了一块空地,规划建设8幢楼,要求每幢楼的面积和层数等都一致,已知该经适房每幢楼每层建筑面积均为250平方米,第一层建筑费用是每平方米3000元,从第二层开始,每一层的建筑费用比其下面一层每平方米增加80元.
(1)若该经适楼房每幢楼共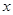 层,总开发费用为
层,总开发费用为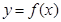 万元,求函数
万元,求函数 的表达式(总开发费用=总建筑费用+购地费用);
的表达式(总开发费用=总建筑费用+购地费用);
(2)要使该批经适房的每平方米的平均开发费用最低,每幢楼应建多少层?
查看答案和解析>>
科目:高中数学 来源:2011-2012年广东省高二上学期期中考试文科数学 题型:解答题
(本题满分14分) 某中学为了解学生的睡眠情况与学习效率的关系,从中抽取20名学生作为样本进行调查.调查的数据整理分组如下表示:
|
睡眠时间(单位:小时) |
|
|
|
|
|
|
|
频 数 |
1 |
3 |
|
6 |
4 |
|
|
频 率 |
|
|
0.20 |
|
|
|
(1)将以上表格补充完整,
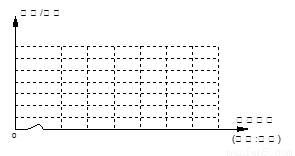
(2)在给定的坐标系内画出样本的频率分布直方图;
(3)为了比较睡眠情况与学习效率的关系,现从睡眠时间在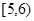 与
与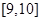 个小时的学生中抽取2人,问能在这两个睡眠时间内各抽到1个学生的概率是多少?
个小时的学生中抽取2人,问能在这两个睡眠时间内各抽到1个学生的概率是多少?
查看答案和解析>>
科目:高中数学 来源:2010年广东省高三第一次月考文科数学卷 题型:解答题
(本题满分14分)
某校高三的某次数学测试中,对其中100名学生的成绩进行分析,按成绩分组,得到的频率分布表如下:
|
组号 |
分组 |
频数 |
频率 |
|
第1组 |
|
15 |
① |
|
第2组 |
|
② |
0.35 |
|
第3组 |
|
20 |
0.20 |
|
第4组 |
|
20 |
0.20 |
|
第5组 |
|
10 |
0.10 |
|
合计 |
|
100 |
1.00 |
(1)求出频率分布表中①、②位置相应的数据;
(2)为了选拔出最优秀的学生参加即将举行的数学竞赛,学校决定在成绩较高的第3、4、5组中分层抽样取5名学生,则第4、5组每组各抽取多少名学生?
(3)为了了解学生的学习情况,学校又在这5名学生当中随机抽取2名进行访谈,求第4组中至少有一名学生被抽到的概率是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com