练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】某公司租赁甲、乙两种设备生产A，B两类产品，甲种设备每天能生产A类产品5件和B类产品10件，乙种设备每天能生产A类产品6件和B类产品20件。已知设备甲每天的租赁费为200元，设备乙每天的租赁费为300元，现该公司至少要生产A类产品50件，B类产品140件，所需租赁费最少为多少元？

    【答案】2300

    【解析】试题分析：设甲种设备需要生产x天，乙种设备需要生产y天，该公司所需租赁费为z元，则，（2分）

    甲、乙两种设备生产A，B两类产品的情况为下表所示：

    产品
    设备

    A类产品
    （件）（≥50）

    B类产品
    （件）（≥140）

    租赁费
    （元）

    甲设备

    5

    10

    200

    乙设备

    6

    20

    300

    （4分）

    则满足的关系为即

    作出不等式表示的平面区域，

    当对应的直线过两直线的交点（4,5）时，目标函数取得最低为2300元。（12分）

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知常数，函数.

    (1)讨论在区间上的单调性；

    (2)若存在两个极值点，且，求a的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=ax（a＞0且a≠1）的图象经过点（2， ）．
    （1）比较f（2）与f（b2+2）的大小；
    （2）求函数g（x）=a （x≥0）的值域．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】以下几个命题中真命题的序号为 ．
    ①在空间中，m、n是两条不重合的直线，α、β是两个不重合的平面，如果α⊥β，α∩β=n，m⊥n，那么m⊥β；
    ②相关系数r的绝对值越接近于1，两个随机变量的线性相关性越强；
    ③用秦九昭算法求多项式f（x）=208+9x2+6x4+x6在x=﹣4时，v2的值为22；
    ④过抛物线y2=4x的焦点作直线与抛物线相交于A、B两点，则使它们的横坐标之和等于4的直线有且只有两条．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图是从成都某中学参加高三体育考试的学生中抽出的40名学生体育成绩（均为整数）的频率分布直方图，该直方图恰好缺少了成绩在区间[70，80）内的图形，根据图形的信息，回答下列问题：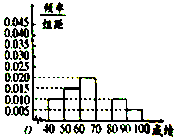
    （1）求成绩在区间[70，80）内的频率，并补全这个频率分布直方图，并估计这次考试的及格率（60分及以上为及格）；
    （2）从成绩在[80，100]内的学生中选出三人，记在90分以上（含90分）的人数为X，求X的分布列及数学期望．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数

    （1）讨论的单调性；

    （2）设，当时，，求的最大值；

    （3）已知，估计的近似值（精确到0.001）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知直线上有一个动点，过点作直线垂直于轴，动点在上，且满足（为坐标原点），记点的轨迹为.

    （I）求曲线的方程；

    （II）若直线是曲线的一条切线，当点到直线的距离最短时，求直线的方程.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】关于x的不等式 ＞1+ （其中k∈R，k≠0）．
    （1）若x=3在上述不等式的解集中，试确定k的取值范围；
    （2）若k＞1时，上述不等式的解集是x∈（3，+∞），求k的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】数列{an}的前n项和Sn=an﹣1，则关于数列{an}的下列说法中，正确的个数有（ ）
    ①一定是等比数列，但不可能是等差数列
    ②一定是等差数列，但不可能是等比数列
    ③可能是等比数列，也可能是等差数列
    ④可能既不是等差数列，又不是等比数列
    ⑤可能既是等差数列，又是等比数列．
    A.4
    B.3
    C.2
    D.1

    查看答案和解析>>

    同步练习册答案