
如图,在四棱锥 中,底面
中,底面 是矩形,
是矩形, 平面
平面 ,
,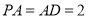 ,
, ,
, 于点
于点 .
.

(1) 求证:
 ;
;
(2) 求直线 与平面
与平面 所成的角的余弦值.
所成的角的余弦值.
(1)答案详见解析;(2)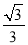
【解析】
试题分析:(1)要证明线线垂直,可考虑先证明直线和平面垂直,该题先证明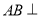 平面
平面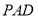 ,从而得到
,从而得到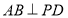 ,又
,又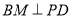 ,故可证明
,故可证明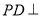 平面
平面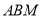 ,进而证明
,进而证明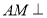
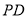 ;(2)求直线和平面所成的角,需先找后求,同时要有必要的证明过程,该题中直线和平面所成的角不易找到,故可采取转化法,先求点
;(2)求直线和平面所成的角,需先找后求,同时要有必要的证明过程,该题中直线和平面所成的角不易找到,故可采取转化法,先求点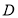 到平面
到平面 的距离
的距离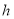 ,再利用
,再利用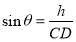 ,求得所求角的正弦值,进而求余弦值.故求点
,求得所求角的正弦值,进而求余弦值.故求点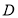 到平面
到平面 的距离成为解题关键,可利用等体积转化法进行.
的距离成为解题关键,可利用等体积转化法进行.
试题解析:(1)证明:∵ 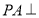 平面
平面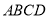 ,
,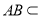 平面
平面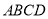 ,∴
,∴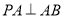 .
.
∵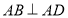 ,
,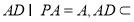 平面
平面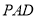 ,
,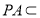 平面
平面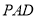 ,
,
∴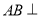 平面
平面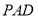 .
.
∵ 平面
平面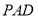
∴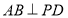 , 3分
, 3分
∵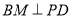 ,
, 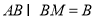 ,
,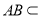 平面
平面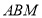 ,
,
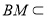 平面
平面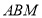 ,∴
,∴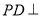 平面
平面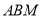 .
.
∵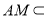 平面
平面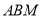 ,∴
,∴
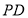 . 6分
. 6分
(2)【解析】
由(1)知,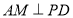 ,又
,又 ,
,
则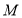 是
是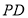 的中点,在Rt△
的中点,在Rt△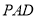 中, 得
中, 得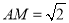 ,
,
在Rt△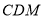 中,得
中,得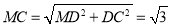 ,
,
∴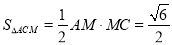 .
.
设点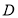 到平面
到平面 的距离为
的距离为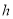 ,由
,由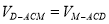 , 8分
, 8分
得 .解得
.解得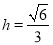 , 10分
, 10分
设直线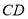 与平面
与平面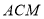 所成的角为
所成的角为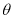 ,
,
则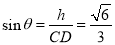 , 12分
, 12分
∴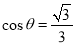 .
.
∴直线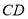 与平面
与平面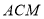 所成的角的余弦值为
所成的角的余弦值为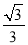 . 14分
. 14分
考点:1、直线和平面垂直的判断;2、直线和平面垂直的性质定理;3、直线和平面所成的角.


科目:高中数学 来源:2013-2014学年浙江省高三高考模拟冲刺卷(提优卷)(二)文科数学试卷(解析版) 题型:选择题
某程序框图如图所示,若该程序运行后输出的值是( )

A.2 B.-2 C.3 D.-3
查看答案和解析>>
科目:高中数学 来源:2013-2014学年浙江省高三高考模拟冲刺卷(提优卷)(三)文科数学试卷(解析版) 题型:选择题
执行如图所示的程序框图,如果输入的N是4,那么输出的p是( )
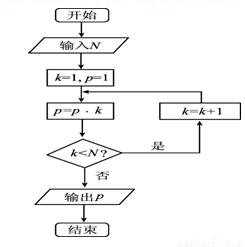
A.6 B.24 C.120 D.720
查看答案和解析>>
科目:高中数学 来源:2013-2014学年浙江省六市六校联盟高考模拟理科数学试卷(解析版) 题型:选择题
已知两个不同的平面 ,
, 和两条不重合的直线
和两条不重合的直线 ,则下列四个命题正确的是( )
,则下列四个命题正确的是( )
A.若 ,则
,则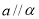
B.若 ,
, ,则
,则
C.若 ,
, ,则
,则
D.若 ,
, ,
,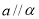 ,则
,则
查看答案和解析>>
科目:高中数学 来源:2013-2014学年浙江省六市六校联盟高考模拟文科数学试卷(解析版) 题型:填空题
如图,正六边形ABCDEF的两个顶点A、D为双曲线的焦点,其余四个顶点都在双曲线上,则该双曲线的离心率为 .
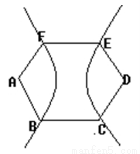
查看答案和解析>>
科目:高中数学 来源:2013-2014学年河南省长葛市毕业班第三次质量预测(三模)理科数学试卷(解析版) 题型:填空题
正三角形ABC的边长为2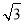 ,将它沿高AD翻折,使点B 与点C间的距离为
,将它沿高AD翻折,使点B 与点C间的距离为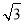 ,此时四面体ABCD的外接球的体积为 。
,此时四面体ABCD的外接球的体积为 。
查看答案和解析>>
科目:高中数学 来源:2013-2014学年河南省郑州市高三第二次模拟考试理科数学试卷(解析版) 题型:填空题
我们把各位数字之和为7的四位数称为“北斗数”(如2014是“北斗数”).则“北斗数”中千位为2的共有 个.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com