
【题目】已知函数![]() (
(![]() ).
).
(1)若![]() ,证明:当
,证明:当![]() 时,
时,![]() ;
;
(2)若对于任意的![]() 且
且![]() ,都有
,都有![]() ,求
,求![]() 的取值集合.
的取值集合.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)将问题转化为当![]() 时,
时,![]() ,利用导数得到
,利用导数得到![]() 的单调性和最值,进行证明;(2)通过函数端值得到
的单调性和最值,进行证明;(2)通过函数端值得到![]() ,将问题等价于当
,将问题等价于当![]() 时,
时,![]() ,对
,对![]() 进行分类,通过导数得到
进行分类,通过导数得到![]() 的单调性,从而得到符合要求的
的单调性,从而得到符合要求的![]() .
.
(1)当![]() 时,
时,![]() ,
,
要证当![]() 时,
时,![]() ,
,
即证当![]() 时,
时,![]()
令![]() ,
,
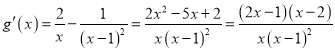
当![]() 时,
时,![]() ,
,![]() 在
在![]() 内单调递减
内单调递减
当![]() 时,
时,![]() ,
,![]() 在
在![]() 内单调递增,
内单调递增,
故![]() .证毕.
.证毕.
(2)先分析端值,当![]() 时,
时,![]() ,
,![]() ,
,
要使![]() ,需有
,需有![]() ,即
,即![]() ;
;
当![]() 时,
时,![]() ,
,![]() ,
,
要使![]() ,需有
,需有![]() ;
;
故必须有![]() .
.
由![]() 知其分子恒正,
知其分子恒正,
令![]() ,
,
于是问题等价于当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() .
.
注意到![]() .
.
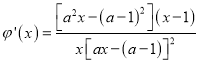
①当![]() 时
时![]() ,
,
此时当![]() 时,
时,![]() ,
,![]() 在
在![]() 单调递减,
单调递减,
于是![]() ,这不符合题意;
,这不符合题意;
②当![]() 时,
时,![]() ,得
,得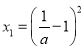 ,
,![]() .
.
(i)当![]() 时,
时,![]() ,
,![]() ,
,![]() 在
在![]() 单调递增,
单调递增,
结合![]() 可知符合题意;
可知符合题意;
(ii)当![]() 时,
时,![]() ,此时当
,此时当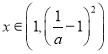 时
时![]() ,
,
于是在![]() 在
在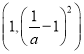 单调递减,
单调递减,
故在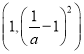 内
内![]() ,这不符合题意;
,这不符合题意;
(iii)当![]() 时,
时,![]() ,此时当
,此时当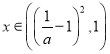 时
时![]() ,
,
于是在![]() 在
在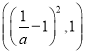 单调递减,
单调递减,
故在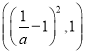 内
内![]() ,这不符合题意;
,这不符合题意;
综上:符合题意的![]() 取值集合为
取值集合为![]() .
.


 学习实践园地系列答案
学习实践园地系列答案科目:高中数学 来源: 题型:
【题目】如图,四棱锥P-ABCD的底面ABCD是菱形,AC与BD交于点O,![]() 底面ABCD,点M为PC中点,
底面ABCD,点M为PC中点,![]() ,
,![]() ,
,![]() .
.
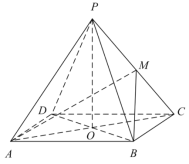
(1)求异面直线AP与BM所成角的余弦值;
(2)求平面ABM与平面PAC所成锐二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数学老师给出一个函数![]() ,甲、乙、丙、丁四个同学各说出了这个函数的一条性质:甲:在
,甲、乙、丙、丁四个同学各说出了这个函数的一条性质:甲:在![]() 上函数单调递减;乙:在
上函数单调递减;乙:在![]() 上函数单调递增;丙:在定义域R上函数的图象关于直线
上函数单调递增;丙:在定义域R上函数的图象关于直线![]() 对称;丁:
对称;丁:![]() 不是函数的最小值.老师说:你们四个同学中恰好有三个人说的正确.那么,你认为____说的是错误的.
不是函数的最小值.老师说:你们四个同学中恰好有三个人说的正确.那么,你认为____说的是错误的.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某大学的![]() 名同学准备拼车去旅游,其中大一、大二、大三、大四每个年级各两名,分乘甲、乙两辆汽车.每车限坐
名同学准备拼车去旅游,其中大一、大二、大三、大四每个年级各两名,分乘甲、乙两辆汽车.每车限坐![]() 名同学(乘同一辆车的
名同学(乘同一辆车的![]() 名同学不考虑位置),其中大一的孪生姐妹需乘同一辆车,则乘坐甲车的
名同学不考虑位置),其中大一的孪生姐妹需乘同一辆车,则乘坐甲车的![]() 名同学中恰有
名同学中恰有![]() 名同学是来自于同一年级的乘坐方式共有_______种(有数字作答).
名同学是来自于同一年级的乘坐方式共有_______种(有数字作答).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在一块耕地上种植一种作物,每季种植成本为1000元,此作物的市场价格和这块地上的产量均具有随机性,且互不影响,其具体情况如下表:
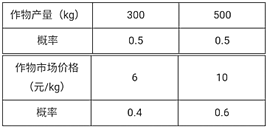
(1)设![]() 表示在这块地上种植1季此作物的利润,求
表示在这块地上种植1季此作物的利润,求![]() 的分布列;
的分布列;
(2)若在这块地上连续3季种植此作物,求这3季中至少有2季的利润不少于2000元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在极坐标系中,曲线C1,C2的极坐标方程分别为ρ=-2cosθ,ρcos![]() =1.
=1.
(1)求曲线C1和C2的公共点的个数;
(2)过极点作动直线与曲线C2相交于点Q,在OQ上取一点P,使|OP|·|OQ|=2,求点P的轨迹,并指出轨迹是什么图形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com