
| A. | C${\;}_{6}^{3}$($\frac{1}{2}$)6 | B. | A${\;}_{4}^{2}$($\frac{1}{2}$)6 | C. | C${\;}_{4}^{2}$($\frac{1}{2}$)6 | D. | C${\;}_{4}^{1}$($\frac{1}{2}$)6 |
分析 根据n次独立重复实验中恰好发生k次的概率,可得这名射手射击3次,再根据相互独立事件的概率乘法公式运算求得结果.
解答 解:根据射手每次射击击中目标的概率是$\frac{1}{2}$,且各次射击的结果互不影响,
故此人射击6次,3次命中的概率为${C}_{6}^{3}$($\frac{1}{2}$)6,
恰有两次连续击中目标的概率为 $\frac{{A}_{4}^{2}}{{C}_{6}^{3}}$,
故此人射击7次,3次命中且恰有2次连续命中的概率为${C}_{6}^{3}$${(\frac{1}{2})}^{6}$•$\frac{{A}_{4}^{2}}{{C}_{6}^{3}}$=${A}_{4}^{2}$${(\frac{1}{2})}^{6}$,
故选:A.
点评 本题主要考查n次独立重复实验中恰好发生k次的概率,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
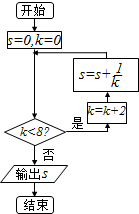
| A. | $\frac{25}{24}$ | B. | $\frac{11}{12}$ | C. | $\frac{5}{6}$ | D. | $\frac{3}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com