
如图,四边形ABEF和ABCD都是直角梯形,∠BAD=∠FAB=90°,BC∥=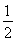 AD,BE∥=
AD,BE∥=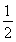 FA,G、H分别为FA、FD的中点.
FA,G、H分别为FA、FD的中点.
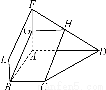
(1)证明:四边形BCHG是平行四边形.
(2)C、D、F、E四点是否共面?为什么?
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第八章第5课时练习卷(解析版) 题型:填空题
已知圆锥的侧面展开图是一个半径为3cm,圆心角为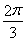 的扇形,则此圆锥的高为________cm.
的扇形,则此圆锥的高为________cm.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第八章第3课时练习卷(解析版) 题型:填空题
已知A、B、C是不共线的三点,直线m垂直于直线AB和AC,直线n垂直于直线BC和AC,则直线m,n的位置关系是________.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第八章第2课时练习卷(解析版) 题型:填空题
过直线l外一点P,作与l平行的平面,则这样的平面有________个.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第八章第1课时练习卷(解析版) 题型:填空题
如图是正四面体的平面展开图,G,H,M,N分别为DE,BE,EF,EC的中点,在这个正四面体中:
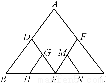
①GH与EF平行;
②BD与MN为异面直线;
③GH与MN成60°角;
④DE与MN垂直.
以上四个命题中,正确命题的是________.(填序号)
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第八章第1课时练习卷(解析版) 题型:填空题
有下列命题:①空间四点共面,则其中必有三点共线;②空间四点不共面,则其中任何三点不共线;③空间四点中有三点共线,则此四点共面;④空间四点中任何三点不共线,则此四点不共面.其中正确的命题是________.(填序号)
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第五章第6课时练习卷(解析版) 题型:填空题
等差数列{an}的前n项和为Sn,已知S10=0,S15=25,则nSn的最小值为________.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第五章第5课时练习卷(解析版) 题型:解答题
已知数列{an}前n项和为Sn,且a2an=S2+Sn对一切正整数都成立.
(1)求a1,a2的值;
(2)设a1>0,数列 前n项和为Tn,当n为何值时,Tn最大?并求出最大值.
前n项和为Tn,当n为何值时,Tn最大?并求出最大值.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第五章第3课时练习卷(解析版) 题型:解答题
在数列{an}中,a1=2,an+1=4an-3n+1,n∈N*.
(1)求证:数列{an-n}是等比数列;
(2)求数列{an}的前n项和Sn;
(3)求证:不等式Sn+1≤4Sn对任意n∈N*皆成立.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com