
【题目】甲、乙两台机床生产同一型号零件.记生产的零件的尺寸为![]() (cm),相关行业质检部门规定:若
(cm),相关行业质检部门规定:若![]() ,则该零件为优等品;若
,则该零件为优等品;若![]() ,则该零件为中等品;其余零件为次品.现分别从甲、乙机床生产的零件中各随机抽取50件,经质量检测得到下表数据:
,则该零件为中等品;其余零件为次品.现分别从甲、乙机床生产的零件中各随机抽取50件,经质量检测得到下表数据:
尺寸 |
|
|
|
|
|
|
甲零件频数 | 2 | 3 | 20 | 20 | 4 | 1 |
乙零件频数 | 3 | 5 | 17 | 13 | 8 | 4 |
(Ⅰ)设生产每件产品的利润为:优等品3元,中等品1元,次品亏本1元.若将频率视为概率,试根据样本估计总体的思想,估算甲机床生产一件零件的利润的数学期望;
(Ⅱ)对于这两台机床生产的零件,在排除其它因素影响的情况下,试根据样本估计总体的思想,估计约有多大的把握认为“零件优等与否和所用机床有关”,并说明理由.
参考公式:![]() .
.
参考数据:
![]()
0.25
0.15
0.10
0.05
0.025
0.010
![]()
1.323
2.072
2.706
3.841
5.024
6.635
【答案】(1)![]() (2)约有
(2)约有![]() 的把握认为“零件优等与否和所用机床有关”.
的把握认为“零件优等与否和所用机床有关”.
【解析】
试题分析:解:(Ⅰ)设甲机床生产一件零件获得的利润为![]() 元,它的分布列为
元,它的分布列为
| 3 | 1 |
|
| 0.8 | 0.14 | 0.06 |
则有![]() =3×0.8+1×0.14+(-1)×0.06=2.48(元).
=3×0.8+1×0.14+(-1)×0.06=2.48(元).
所以,甲机床生产一件零件的利润的数学期望为2.48元.
(Ⅱ)由表中数据可知:甲机床优等品40个,非优等品10个;乙机床优等品30个,非优等品20个.
制作2×2列联表如下:
甲机床 | 乙机床 | 合计 | |
优等品 | 40 | 30 | 70 |
非优等品 | 10 | 20 | 30 |
合计 | 50 | 50 | 100 |
计算![]() =
=![]() .
.
考察参考数据并注意到![]() ,可知:对于这两台机床生产的零件,在排除其它因素影响的情况下,根据样本估计总体的思想,约有95%的把握认为“零件优等与否和所用机床有关”.
,可知:对于这两台机床生产的零件,在排除其它因素影响的情况下,根据样本估计总体的思想,约有95%的把握认为“零件优等与否和所用机床有关”.


科目:高中数学 来源: 题型:
【题目】在直角坐标平面内,以坐标原点![]() 为极点,
为极点,![]() 轴的非负半轴为极轴建立极坐标系.已知曲线
轴的非负半轴为极轴建立极坐标系.已知曲线![]() 的极坐标方程为
的极坐标方程为![]() ,直线
,直线![]() 的参数方程为
的参数方程为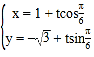 (
(![]() 为参数).
为参数).
(1)分别求出曲线![]() 和直线
和直线![]() 的直角坐标方程;
的直角坐标方程;
(2)若点![]() 在曲线
在曲线![]() 上,且
上,且![]() 到直线
到直线![]() 的距离为1,求满足这样条件的点
的距离为1,求满足这样条件的点![]() 的个数.
的个数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax2+bx+c(a>0),且f(1)![]() .
.
(1)求证:函数f(x)有两个不同的零点;
(2)设x1,x2是函数f(x)的两个不同的零点,求|x1﹣x2|的取值范围;
(3)求证:函数f(x)在区间(0,2)内至少有一个零点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)求函数![]() 的对称轴方程;
的对称轴方程;
(2)将函数![]() 的图象上各点的纵坐标保持不变,横坐标伸长为原来的2倍,然后再向左平移
的图象上各点的纵坐标保持不变,横坐标伸长为原来的2倍,然后再向左平移![]() 个单位,得到函数
个单位,得到函数![]() 的图象.若
的图象.若![]() ,
, ![]() ,
, ![]() 分别是
分别是![]() △三个内角
△三个内角![]() ,
, ![]() ,
, ![]() 的对边,
的对边, ![]() ,
, ![]() ,且
,且![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,直线l1:kx-y+4=0与直线l2:x+ky-3=0相交于点P,则当实数k变化时,点P到直线4x-3y+10=0的距离的最大值为( )
A.2B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率
的离心率![]() ,左、右焦点分别为
,左、右焦点分别为![]() ,且
,且![]() 与抛物线
与抛物线![]() 的焦点重合.
的焦点重合.
(1)求椭圆的标准方程;
(2)若过![]() 的直线交椭圆于
的直线交椭圆于![]() 两点,过
两点,过![]() 的直线交椭圆于
的直线交椭圆于![]() 两点,且
两点,且![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个袋中装有四个形状大小完全相同的球,球的编号分别为1,2,3,4.
(1)从袋中随机抽取两个球,求取出的球的编号之和不大于4的概率;
(2)先从袋中随机取一个球,该球的编号为m,将球放回袋中,然后再从袋中随机取一个球,该球的编号为n,求![]() 的概率
的概率
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com