
【题目】已知椭圆C:![]() (
(![]() )的一个焦点与抛物线
)的一个焦点与抛物线![]() 的焦点相同,
的焦点相同,![]() ,
,![]() 为椭圆的左、右焦点,M为椭圆上任意一点,若
为椭圆的左、右焦点,M为椭圆上任意一点,若![]() 的面积最大值为1.
的面积最大值为1.
(1)求椭圆C的方程;
(2)设不过原点的直线l:![]() 与椭圆C交于不同的两点A、B,若直线l的斜率是直线
与椭圆C交于不同的两点A、B,若直线l的斜率是直线![]() 、
、![]() 斜率的等比中项,求
斜率的等比中项,求![]() 面积的取值范围.
面积的取值范围.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
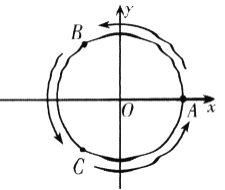
【题目】如图,直角坐标系中,圆的方程为![]() ,
,![]() ,
,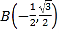 ,
,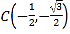 为圆上三个定点,某同学从
为圆上三个定点,某同学从![]() 点开始,用掷骰子的方法移动棋子.规定:①每掷一次骰子,把一枚棋子从一个定点沿圆弧移动到相邻下一个定点;②棋子移动的方向由掷骰子决定,若掷出骰子的点数为偶数,则按图中箭头方向移动;若掷出骰子的点数为奇数,则按图中箭头相反的方向移动.设掷骰子
点开始,用掷骰子的方法移动棋子.规定:①每掷一次骰子,把一枚棋子从一个定点沿圆弧移动到相邻下一个定点;②棋子移动的方向由掷骰子决定,若掷出骰子的点数为偶数,则按图中箭头方向移动;若掷出骰子的点数为奇数,则按图中箭头相反的方向移动.设掷骰子![]() 次时,棋子移动到
次时,棋子移动到![]() ,
,![]() ,
,![]() 处的概率分别为
处的概率分别为![]() ,
,![]() ,
,![]() .例如:掷骰子一次时,棋子移动到
.例如:掷骰子一次时,棋子移动到![]() ,
,![]() ,
,![]() 处的概率分别为
处的概率分别为![]() ,
,![]() ,
,![]() .
.
(1)分别掷骰子二次,三次时,求棋子分别移动到![]() ,
,![]() ,
,![]() 处的概率;
处的概率;
(2)掷骰子![]() 次时,若以
次时,若以![]() 轴非负半轴为始边,以射线
轴非负半轴为始边,以射线![]() ,
,![]() ,
,![]() 为终边的角的余弦值记为随机变量
为终边的角的余弦值记为随机变量![]() ,求
,求![]() 的分布列和数学期望;
的分布列和数学期望;
(3)记![]() ,
,![]() ,
,![]() ,其中
,其中![]() .证明:数列
.证明:数列![]() 是等比数列,并求
是等比数列,并求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),将曲线
为参数),将曲线![]() 上每一点的横坐标变为原来的
上每一点的横坐标变为原来的![]() 倍,纵坐标不变,得到曲线
倍,纵坐标不变,得到曲线![]() ,以坐标原点
,以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,射线
轴的正半轴为极轴建立极坐标系,射线![]() 与曲线
与曲线![]() 交于点
交于点![]() ,将射线
,将射线![]() 绕极点逆时针方向旋转
绕极点逆时针方向旋转![]() 交曲线
交曲线![]() 于点
于点![]() .
.
(1)求曲线![]() 的参数方程;
的参数方程;
(2)求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系x![]() y中,曲线C的参数方程为
y中,曲线C的参数方程为![]() 为参数),在以
为参数),在以![]() 为极点,
为极点,![]() 轴的非负半轴为极轴的极坐标系中,直线
轴的非负半轴为极轴的极坐标系中,直线![]() 的极坐标方程为
的极坐标方程为![]() 。
。
(1)求曲线C的极坐标方程;
(2)设直线![]() 与曲线C相交于A,B两点,P为曲C上的一动点,求△PAB面积的最大值.
与曲线C相交于A,B两点,P为曲C上的一动点,求△PAB面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】共享单车的投放,方便了市民短途出行,被誉为中国“新四大发明”之一.某市为研究单车用户与年龄的相关程度,随机调查了100位成人市民,统计数据如下:
不小于40岁 | 小于40岁 | 合计 | |
单车用户 | 12 | y | m |
非单车用户 | x | 32 | 70 |
合计 | n | 50 | 100 |
(1)求出列联表中字母x、y、m、n的值;
(2)①从此样本中,对单车用户按年龄采取分层抽样的方法抽出5人进行深入调研,其中不小于40岁的人应抽多少人?
②从独立性检验角度分析,能否有![]() 以上的把握认为该市成人市民是否为单车用户与年龄是否小于40岁有关.
以上的把握认为该市成人市民是否为单车用户与年龄是否小于40岁有关.
下面临界值表供参考:
P( | 0.15 | 0.10 | 0.05 | 0.25 | 0.010 | 0.005 | 0.001 |
k | 2.072 | 2.706 | 3.841 | 5.024 | 6635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年是五四运动100周年.五四运动以来的100年,是中国青年一代又一代接续奋斗、凯歌前行的100年,是中口青年用青春之我创造青春之中国、青春之民族的100年.为继承和发扬五四精神在青年节到来之际,学校组织“五四运动100周年”知识竞赛,竞赛的一个环节由10道题目组成,其中6道A类题、4道B类题,参赛者需从10道题目中随机抽取3道作答,现有甲同学参加该环节的比赛.
(1)求甲同学至少抽到2道B类题的概率;
(2)若甲同学答对每道A类题的概率都是![]() ,答对每道B类题的概率都是
,答对每道B类题的概率都是![]() ,且各题答对与否相互独立.现已知甲同学恰好抽中2道A类题和1道B类题,用X表示甲同学答对题目的个数,求随机变量X的分布列和数学期望.
,且各题答对与否相互独立.现已知甲同学恰好抽中2道A类题和1道B类题,用X表示甲同学答对题目的个数,求随机变量X的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国南北朝数学家何承天发明的“调日法”是程序化寻求精确分数来表示数值的算法,其理论依据是:设实数![]() 的不足近似值和过剩近似值分别为
的不足近似值和过剩近似值分别为![]() 和
和![]() ,则
,则![]() 是
是![]() 的更为精确的不足近似值或过剩近似值.我们知道
的更为精确的不足近似值或过剩近似值.我们知道![]() ,若令
,若令![]() ,则第一次用“调日法”后得
,则第一次用“调日法”后得![]() 是
是![]() 的更为精确的过剩近似值,即
的更为精确的过剩近似值,即![]() ,若每次都取最简分数,那么第四次用“调日法”后可得
,若每次都取最简分数,那么第四次用“调日法”后可得![]() 的近似分数为( )
的近似分数为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在![]() 中,
中,![]() ,
,![]() .已知
.已知![]() 分别是
分别是![]() 的中点.将
的中点.将![]() 沿
沿![]() 折起,使
折起,使![]() 到
到![]() 的位置且二面角
的位置且二面角![]() 的大小是60°,连接
的大小是60°,连接![]() ,如图:
,如图:
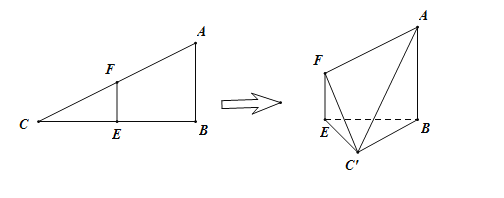
(1)证明:平面![]() 平面
平面![]()
(2)求平面![]() 与平面
与平面![]() 所成二面角的大小.
所成二面角的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com