
【题目】水培植物需要一种植物专用营养液,已知每投放![]() (
(![]() 且
且![]() )个单位的营养液,它在水中释放的浓度
)个单位的营养液,它在水中释放的浓度![]() (克/升)随着时间
(克/升)随着时间![]() (天)变化的函数关系式近似为
(天)变化的函数关系式近似为![]() ,其中
,其中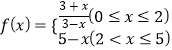 ,若多次投放,则某一时刻水中的营养液浓度为每次投放的营养液在相应时刻所释放的浓度之和,根据经验,当水中营养液的浓度不低于4(克/升)时,它才能有效.
,若多次投放,则某一时刻水中的营养液浓度为每次投放的营养液在相应时刻所释放的浓度之和,根据经验,当水中营养液的浓度不低于4(克/升)时,它才能有效.
(1)若只投放一次2个单位的营养液,则有效时间最多可能达到几天?
(2)若先投放2个单位的营养液,3天后再投放![]() 个单位的营养液,要使接下来的2天中,营养液能够持续有效,试求
个单位的营养液,要使接下来的2天中,营养液能够持续有效,试求![]() 的最小值.
的最小值.
【答案】(1)3(2)![]()
【解析】
(Ⅰ)营养液有效则需满足![]() ,由分段函数,对
,由分段函数,对![]() 讨论,解不等式即可得到结论;
讨论,解不等式即可得到结论;
(Ⅱ)设第二次投放营养液的持续时间为![]() 天,则此时第一次投放营养液的持续时间为
天,则此时第一次投放营养液的持续时间为![]() 天,且
天,且![]() ;设设
;设设![]() 为第一次投放营养液的浓度,
为第一次投放营养液的浓度, ![]() 为第二次投放营养液的浓度,
为第二次投放营养液的浓度, ![]() 为水中的营养液的浓度;;可得
为水中的营养液的浓度;;可得![]() 在
在![]() 上恒成立,运用参数分离和换元法,结合基本不等式,即可得到
上恒成立,运用参数分离和换元法,结合基本不等式,即可得到![]() 的最小值.
的最小值.
(1)营养液有效则需满足![]() ,
,
则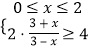 或
或![]() ,
,
即为![]() 或
或![]() ,
,
解得![]() ,
,
所以营养液有效时间最多可达3天;
(2)设第二次投放营养液的持续时间为![]() 天,
天,
则此时第一次投放营养液的持续时间为![]() 天,且
天,且![]() ;
;
设![]() 为第一次投放营养液的浓度,
为第一次投放营养液的浓度, ![]() 为第二次投放营养液的浓度,
为第二次投放营养液的浓度, ![]() 为水中的营养液的浓度;
为水中的营养液的浓度;
∴![]() ,
,
![]() ,
,
由题意得![]() 在
在![]() 上恒成立,
上恒成立,
∴![]() 在
在![]() 上恒成立,
上恒成立,
令![]() ,则
,则![]() ,
,
又![]() ,
,
当且仅当![]() ,即
,即![]() 时等号成立;
时等号成立;
因为![]()
所以![]() 的最小值为
的最小值为![]() .
.


 互动英语系列答案
互动英语系列答案 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案科目:高中数学 来源: 题型:
【题目】公元263年左右,我国数学家刘徽发现,当圆内接多边形的边数无限增加时,多边形面积可无限逼近圆的面积,由此创立了割圆术,利用割圆术刘徽得到了圆周率精确到小数点后面两位的近似值3.14,这就是著名的徽率.如图是利用刘徽的割圆术设计的程序框图,则输出的n值为 (参考数据:![]() ,
,![]() ,
,![]() )
)

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某财经频道报道了某地建筑市场存在违规使用未经淡化海砂的现象.为了研究使用淡化海砂与混凝土耐久性是否达标有关,某大学实验室随机抽取了60个样本,得到了相关数据如下表:
混凝土耐久性达标 | 混凝土耐久性不达标 | 总计 | |
使用淡化海砂 | 25 | t | 30 |
使用未经淡化海砂 | s | 15 | 30 |
总计 | 40 | 20 | 60 |
(Ⅰ)根据表中数据,求出s,t的值,利用独立性检验的方法判断,能否在犯错误的概率不超过1%的前提下认为使用淡化海砂与混凝土耐久性是否达标有关?
(Ⅱ)若用分层抽样的方法在使用淡化海砂的样本中抽取了6个,现从这6个样本中任取2个,则取出的2个样本混凝土耐久性都达标的概率是多少?
参考数据:
P(K2≥k0) | 0.10 | 0.050 | 0.025 | 0.010 | 0.001 |
k0 | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
参考公式:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市化工厂三个车间共有工人1 000名,各车间男、女工人数如下表:
第一车间 | 第二车间 | 第三车间 | |
女工 | 173 | 100 | y |
男工 | 177 | x | z |
已知在全厂工人中随机抽取1名,抽到第二车间男工的可能性是0. 15.
(1)求x的值;
(2)现用分层抽样的方法在全厂抽取50名工人,问应在第三车间抽取多少名?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2017年5月,“一带一路”沿线的20国青年评选出了中国“新四大发明”:高铁、支付宝、共享单车和网购.2017年末,“支付宝大行动”用发红包的方法刺激支付宝的使用.某商家统计前5名顾客扫描红包所得金额分别为5.5元,2.1元,3.3元,5.9元,4.7元,商家从这5名顾客中随机抽取3人赠送台历.
(1)求获得台历的三人中至少有一人的红包超过5元的概率;
(2)统计一周内每天使用支付宝付款的人数![]() 与商家每天的净利润
与商家每天的净利润![]() 元,得到7组数据,如表所示,并作出了散点图.
元,得到7组数据,如表所示,并作出了散点图.

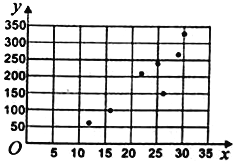
(i)直接根据散点图判断,![]() 与
与![]() 哪一个适合作为每天的净利润的回归方程类型.(
哪一个适合作为每天的净利润的回归方程类型.(![]() 的值取整数)
的值取整数)
(ii)根据(i)的判断,建立![]() 关于
关于![]() 的回归方程,并估计使用支付宝付款的人数增加到35时,商家当天的净利润.
的回归方程,并估计使用支付宝付款的人数增加到35时,商家当天的净利润.
参考数据:
|
|
|
|
22.86 | 194.29 | 268.86 | 3484.29 |
附:对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为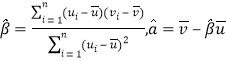 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】据统计ABO血型具有民族和地区差异.在我国H省调查了30488人,四种血型的人数如下:
血型 | A | B | O | AB |
人数/人 | 7704 | 10765 | 8970 | 3049 |
频率 |
(1)计算H省各种血型的频率并填表(精确到0.001);
(2)如果从H省任意调查一个人的血型,那么他是O型血的概率大约是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,椭圆![]() 的中心为坐标原点,焦点
的中心为坐标原点,焦点![]() ,
,![]() 在
在![]() 轴上,且
轴上,且![]() 在抛物线
在抛物线![]() 的准线上,点
的准线上,点![]() 是椭圆
是椭圆![]() 上的一个动点,
上的一个动点,![]() 面积的最大值为
面积的最大值为![]() .
.

(1)求椭圆![]() 的方程;
的方程;
(2)过焦点![]() ,
,![]() 作两条平行直线分别交椭圆
作两条平行直线分别交椭圆![]() 于
于![]() ,
,![]() ,
,![]() ,
,![]() 四个点.求四边形
四个点.求四边形![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com