
【题目】某学校为了了解学生使用手机的情况,分别在高一和高二两个年级各随机抽取了100名学生进行调查.下面是根据调查结果绘制的学生日均使用手机时间的频数分布表和频率分布直方图,将使用手机时间不低于80分钟的学生称为“手机迷”.

高一学生日均使用手机时间的频数分布表
时间分组 | 频数 |
[0,20) | 12 |
[20,40) | 20 |
[40,60) | 24 |
[60,80) | 18 |
[80,100) | 22 |
[100,120] | 4 |
(1)将频率视为概率,估计哪个年级的学生是“手机迷”的概率大?请说明理由.
(2)在高二的抽查中,已知随机抽到的女生共有55名,其中10名为“手机迷”.根据已知条件完成下面的2×2列联表,并据此资料你有多大的把握认为“手机迷”与性别有关?
非手机迷 | 手机迷 | 合计 | |
男 | |||
女 | |||
合计 |
附:随机变量 (其中
(其中![]() 为样本总量).
为样本总量).
参考数据 |
| 0.15 | 0.10 | 0.05 | 0.025 |
| 2.072 | 2.706 | 3.841 | 5.024 |
【答案】(1) 高一年级的学生是“手机迷”的概率大;(2) 有90%的把握认为“手机迷”与性别有关.
【解析】
试题分析:(1)由频率分布直方图分别计算高一学生与高二学生手机谜的概率,并比较大小即可;(2)根据频率分布直方图求出在抽取的100人中“手机谜”与“非手机谜”中男、女人数,填入列联表,代入公式计算观察值![]() ,与参考数据表格对比即可.
,与参考数据表格对比即可.
试题解析: (1)由频数分布表可知,高一学生是“手机迷”的概率为![]()
由频率分布直方图可知,高二学生是“手机迷”的概率为![]() =(0.0025+0.010)×20=0.25
=(0.0025+0.010)×20=0.25
因为P1>P2,所以高一年级的学生是“手机迷”的概率大.
(2)由频率分布直方图可知,在抽取的100人中,
“手机迷”有(0.010+0.0025)×20×100=25(人),
非手机迷有100﹣25=75(人).
从而2×2列联表如下:
非手机迷 | 手机迷 | 合计 | |
男 | 30 | 15 | 45 |
女 | 45 | 10 | 55 |
合计 | 75 | 25 | 100 |
将2×2列联表中的数据代入公式计算,
得![]()
因为3.030>2.706,所以有90%的把握认为“手机迷”与性别有关.


科目:高中数学 来源: 题型:
【题目】某河上有座抛物线型拱桥,当水面距拱顶5m时水面宽为8m,一木船宽为4m,高为2m,载货后木船露在水面上的部分高为0.75m,问水面上涨到与拱顶相距多少时,木船开始不能通过。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在一个盒子里装有6张卡片,上面分别写着如下定义域为![]() 的函数:
的函数:
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
(1)现在从盒子中任意取两张卡片,记事件![]() 为“这两张卡片上函数相加,所得新函数是奇函数”,求事件
为“这两张卡片上函数相加,所得新函数是奇函数”,求事件![]() 的概率;
的概率;
(2)从盒中不放回逐一抽取卡片,若取到一张卡片上的函数是偶函数则停止抽取,否则继续进行,记停止时抽取次数为![]() ,写出
,写出![]() 的分布列,并求其数学期望
的分布列,并求其数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若<<0,则下列不等式:①<;②|a|+b>0;③a->b-;④lna2>lnb2中,正确的是( )
(A)①④ (B)②③ (C)①③ (D)②④
查看答案和解析>>
科目:高中数学 来源: 题型:
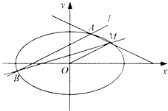
【题目】如图,椭圆![]() :
:![]() (
(![]() )的短轴长为
)的短轴长为![]() ,点
,点![]() 在C上,平行于OM的直线
在C上,平行于OM的直线![]() 交椭圆C于不同的两点A,B.
交椭圆C于不同的两点A,B.
(1)求椭圆![]() 的方程;
的方程;
(2)证明:直线MA,MB与![]() 轴总围成等腰三角形.
轴总围成等腰三角形.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】连江一中第49届田径运动会提出了“我运动、我阳光、我健康、我快乐”的口号,某同学要设计一张如图所示的竖向张贴的长方形海报进行宣传,要求版心面积为162 ![]() (版心是指图中的长方形阴影部分,
(版心是指图中的长方形阴影部分,![]() 为长度单位分米),上、下两边各空2
为长度单位分米),上、下两边各空2 ![]() ,左、右两边各空1
,左、右两边各空1 ![]() .
.

(1)若设版心的高为![]()
![]() ,求海报四周空白面积关于
,求海报四周空白面积关于![]() 的函数
的函数![]() 的解析式;
的解析式;
(2)要使海报四周空白面积最小,版心的高和宽该如何设计?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com