
【题目】已知两曲线f(x)= ![]() x2+ax与g(x)=2a2lnx+b有公共点,且在该点处有相同的切线,则a∈(0,+∞)时,实数b的最大值是( )
x2+ax与g(x)=2a2lnx+b有公共点,且在该点处有相同的切线,则a∈(0,+∞)时,实数b的最大值是( )
A.e ![]()
B.2e ![]()
C.e ![]()
D.![]() e
e ![]()
【答案】A
【解析】解:f(x)= ![]() x2+ax与g(x)=2a2lnx+b, 设y=f(x)与y=g(x)(x>0)在公共点(x0 , y0)处的切线相同、
x2+ax与g(x)=2a2lnx+b, 设y=f(x)与y=g(x)(x>0)在公共点(x0 , y0)处的切线相同、
f′(x)=x+a,g′(x)= ![]() ,
,
由题意f(x0)=g(x0),f′(x0)=g′(x0),
即 ![]() x02+ax0=2a2lnx0+b,x0+a=
x02+ax0=2a2lnx0+b,x0+a= ![]() ,
,
得x0=a或x0=﹣2a(舍去),
即有b= ![]() a2+a2﹣2a2lna=
a2+a2﹣2a2lna= ![]() a2﹣2a2lna.
a2﹣2a2lna.
令h(t)= ![]() t2﹣2t2lnt(t>0),
t2﹣2t2lnt(t>0),
则h′(t)=t(1﹣4lnt)、
于是当t(1﹣4lnt)>0,即0<t<e ![]() 时,h′(t)>0;
时,h′(t)>0;
当t(1﹣4lnt)<0,即t>e ![]() 时,h′(t)<0.
时,h′(t)<0.
故h(t)在(0,e ![]() )为增函数,在(e
)为增函数,在(e ![]() ,+∞)为减函数,
,+∞)为减函数,
于是h(t)在(0,+∞)的最大值为h(e ![]() )=
)= ![]() e
e ![]() ﹣2e
﹣2e ![]()
![]() =e
=e ![]() ,
,
故b的最大值为e ![]() .
.
故选:A.


 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案科目:高中数学 来源: 题型:
【题目】已知双曲线C: ![]() =1(a>0,b>0)的离心率为
=1(a>0,b>0)的离心率为 ![]() ,实轴长为2,直线l:x﹣y+m=0与双曲线C交于不同的两点A,B,
,实轴长为2,直线l:x﹣y+m=0与双曲线C交于不同的两点A,B,
(1)求双曲线C的方程;
(2)若线段AB的中点在圆x2+y2=5上,求m的值;
(3)若线段AB的长度为4 ![]() ,求直线l的方程.
,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱ABC﹣A1B1C1中,AC=3,BC=4,AB=5,AA1=4,点D是AB的中点. 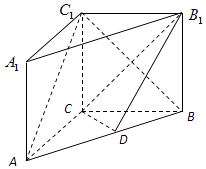
(1)求证:AC⊥BC1;
(2)求证:AC1∥平面CDB1;
(3)求二面角B﹣DC﹣B1的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=lnx﹣ax,g(x)=ex﹣3ax,其中a为实数,若f(x)在(1,+∞)上是单调减函数,且g(x)在(1,+∞)上有最小值,则a的取值范围是( )
A.( ![]() ,+∞)
,+∞)
B.[ ![]() ,+∞)
,+∞)
C.(1,+∞)
D.[1,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在R上的函数f(x)= ![]() x3+cx+3(c为常数),f(x)在x=0处的切线与直线y=x+2垂直.
x3+cx+3(c为常数),f(x)在x=0处的切线与直线y=x+2垂直.
(1)求函数y=f(x)的解析式;
(2)设g(x)=4lnx﹣f′(x),(其中f′(x)是函数f(x)的导函数),求g(x)的极值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ex , g(x)=mx2+ax+b,其中m,a,b∈R,e=2.71828…为自然对数的底数. (I)函数h(x)=xf (x),当a=l,b=0时,若函数h(x)与g(x)具有相同的单调区间,求m的值;
(II)记F(x)=f(x)﹣g(x).当a=2,m=0时,若函数F(x)在[﹣1,2]上存在两个不同的零点,求b的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两位打字员在两台电脑上各自输入A,B两种类型的文件的部分文字才能使这两类文件成为成品.已知A文件需要甲输入0.5小时,乙输入0.2小时;B文件需要甲输入0.3小时,乙输入0.6小时.在一个工作日中,甲至多只能输入6小时,乙至多只能输入8小时,A文件每份的利润为60元,B文件每份的利润为80元,则甲、乙两位打字员在一个工作日内获得的最大利润是元.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com