
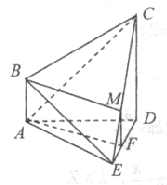
【题目】如图,在四棱锥E-ABCD中,AE⊥DE,CD⊥平面ADE,AB⊥平面ADE,CD=DA=6,AB=2,DE=3.
(I)求棱锥C-ADE的体积;
(II)求证:平面ACE⊥平面CDE;
(III)在线段DE上是否存在一点F,使AF∥平面BCE?若存在,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.

【答案】(Ⅰ) ![]() ;(Ⅱ)证明见解析;(Ⅲ)答案见解析.
;(Ⅱ)证明见解析;(Ⅲ)答案见解析.
【解析】试题分析:(I)在![]() 中,
中, ![]() ,可得
,可得![]() ,由于
,由于![]() 平面
平面![]() ,可得
,可得![]() ;(II)由
;(II)由![]() 平面
平面![]() ,可得
,可得![]() ,进而得到
,进而得到![]() 平面
平面![]() ,即可证明平面
,即可证明平面![]() 平面
平面![]() ;(III)在线段
;(III)在线段![]() 上存在一点
上存在一点![]() ,使
,使![]() 平面
平面![]() ,
, ![]() .设
.设![]() 为线段
为线段![]() 上的一点,且
上的一点,且![]() ,过
,过![]() 作
作![]() 交
交![]() 于点
于点![]() ,由线面垂直的性质可得:
,由线面垂直的性质可得: ![]() .可得四边形
.可得四边形![]() 是平行四边形,于是
是平行四边形,于是![]() ,即可证明
,即可证明![]() 平面
平面![]()
试题解析:(I)在Rt△ADE中, ![]() ,因为CD⊥平面ADE,
,因为CD⊥平面ADE,
所以棱锥C-ADE的体积为![]() .
.
(II)因为![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,所以
,所以![]() .又因为
.又因为![]() ,
, ![]() ,所以
,所以![]() 平面
平面![]() ,又因为
,又因为![]() 平面
平面![]() ,所以平面
,所以平面![]() 平面
平面![]()
(III)在线段![]() 上存在一点F,且
上存在一点F,且![]() ,使
,使![]() 平面
平面![]() .
.
解:设![]() 为线段
为线段![]() 上一点,且
上一点,且![]() ,过点
,过点![]() 作
作![]() 交
交![]() 于
于![]() ,则
,则![]() .
.
因为![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,所以
,所以![]() ,又因为
,又因为![]()
所以![]() ,
, ![]() ,所以四边形
,所以四边形![]() 是平行四边形,则
是平行四边形,则![]() .
.
又因为![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】如图,在直角坐标系![]() 中,椭圆
中,椭圆![]() :
: ![]()
![]() 的上焦点为
的上焦点为![]() ,椭圆
,椭圆![]() 的离心率为
的离心率为![]() ,且过点
,且过点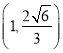 .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设过椭圆![]() 的上顶点
的上顶点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于点
交于点![]() (
(![]() 不在
不在![]() 轴上),垂直于
轴上),垂直于![]() 的直线与
的直线与![]() 交于点
交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,若
,若![]() ,且
,且![]() ,求直线
,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知四棱锥![]() 的底面的菱形,
的底面的菱形, ![]() ,点E是BC边的中点,AC和DE交于点O,PO
,点E是BC边的中点,AC和DE交于点O,PO ![]() ;
;
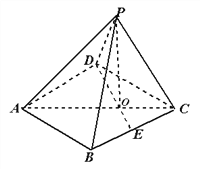
(1)求证: ![]() ;
;
(2)![]() 求二面角P-AD-C的大小。
求二面角P-AD-C的大小。
(3)在(2)的条件下,求异面直线PB与DE所成角的余弦值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2017年“双11”前夕,某市场机构随机对中国公民进行问卷调查,用于调研“双11”民众购物意愿和购物预计支出状况. 分类统计后,从有购物意愿的人中随机抽取100人作为样本,将他(她)们按照购物预计支出(单位:千元)分成8组: [0, 2),[2, 4),[4, 6),…,[14, 16],并绘制成如图所示的频率分布直方图,其中,样本中购物预计支出不低于1万元的人数为a.
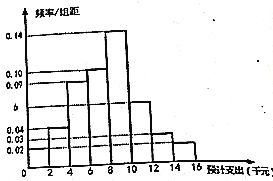
(Ⅰ) (i)求a的值,并估算这100人购物预计支出的平均值;
(ii)以样本估计总体,在有购物意愿的人群中,若至少有65%的人购物预计支出不低于x千元,求x的最大值.
(Ⅱ) 如果参与本次问卷调查的总人数为t,问卷调查得到下列信息:
①参与问卷调查的男女人数之比为2:3;
②男士无购物意愿和有购物意愿的人数之比是1:3,女士无购物意愿和有购物意愿的人数之比为1:4;
③能以90%的把握认为“双11购物意愿与性别有关”,但不能以95%的把握认为“双11购物意愿与性别有关”.
根据以上数据信息,求t所有可能取值组成的集合M.
附: 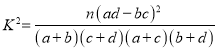 ,其中
,其中![]() .
.
独立检验临界值表:
| 0.100 | 0.050 | 0.025 | 0.010 |
| 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等腰梯形![]() 中(如图1),
中(如图1),![]() ,
, ![]() ,
, ![]() 为线段
为线段![]() 的中点,
的中点, ![]() 为线段
为线段![]() 上的点,
上的点, ![]() ,现将四边形
,现将四边形![]() 沿
沿![]() 折起(如图2).
折起(如图2).
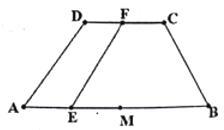
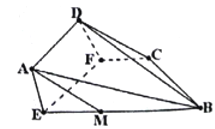
图1 图2
⑴求证: ![]() 平面
平面![]() ;
;
⑵在图2中,若![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和为Sn,满足Sn=2an-1.(n∈N*)
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)若数列{bn}满足bn=![]() an,求数列{bn}的前n项和Tn.
an,求数列{bn}的前n项和Tn.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着网络时代的进步,流量成为手机的附带品,人们可以利用手机随时随地的浏览网页,聊天,看视频,因此,社会上产生了很多低头族.某研究人员对该地区18∽50岁的5000名居民在月流量的使用情况上做出调查,所得结果统计如下图所示:
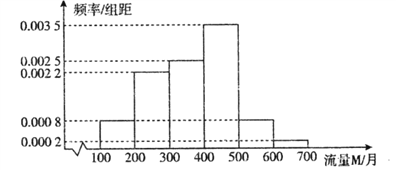
(Ⅰ)以频率估计概率,若在该地区任取3位居民,其中恰有![]() 位居民的月流量的使用情况
位居民的月流量的使用情况
在300M∽400M之间,求![]() 的期望
的期望![]() ;
;
(Ⅱ)求被抽查的居民使用流量的平均值;
(Ⅲ)经过数据分析,在一定的范围内,流量套餐的打折情况![]() 与其日销售份数
与其日销售份数![]() 成线性相关
成线性相关
关系,该研究人员将流量套餐的打折情况![]() 与其日销售份数
与其日销售份数![]() 的结果统计如下表所示:
的结果统计如下表所示:
折扣 | 1折 | 2折 | 3折 | 4折 | 5折 |
销售份数 | 50 | 85 | 115 | 140 | 160 |
试建立![]() 关于
关于![]() 的的回归方程.
的的回归方程.
附注:回归方程![]() 中斜率和截距的最小二乘估计公式分别为:
中斜率和截距的最小二乘估计公式分别为:
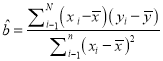 ,
, ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现有m个(![]() )实数
)实数![]() ,它们满足下列条件:①
,它们满足下列条件:①![]() ,
,
②![]() 记这m个实数
记这m个实数![]() 的和为
的和为![]() ,
,
即![]() .
.
(1)若![]() ,证明:
,证明: ![]() ;
;
(2)若m=5,满足题设条件的5个实数构成数列![]() .设C为所有满足题设条件的数列
.设C为所有满足题设条件的数列![]() 构成的集合.集合
构成的集合.集合![]() ,求A中所有正数之和;
,求A中所有正数之和;
(3)对满足题设条件的m个实数构成的两个不同数列![]() 与
与![]() ,证明:
,证明: ![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com