
【题目】我国是世界上严重缺水的国家之一,城市缺水问题较为突出.某市为了节约生活用水,计划在本市试行居民生活用水定额管理(即确定一个居民月均用水量标准:用水量不超过a的部分按照平价收费,超过a的部分按照议价收费).为了较为合理地确定出这个标准,通过抽样获得了100位居民某年的月均用水量(单位:吨),制作了频率分布直方图,
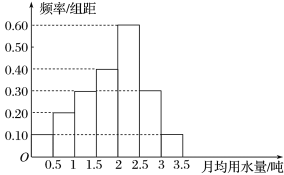
(Ⅰ)用该样本估计总体:
(1)估计该市居民月均用水量的平均数;
(2)如果希望86%的居民每月的用水量不超出标准,则月均用水量a的最低标准定为多少吨?
(Ⅱ)若将频率视为概率,现从该市某大型生活社区随机调查3位居民的月均用水量,其中月均用水量不超过2.5吨的人数为X,求X的分布列和均值.
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中已知椭圆
中已知椭圆![]() 过点
过点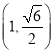 ,其左、右焦点分别为
,其左、右焦点分别为![]() ,离心率为
,离心率为![]() .
.
(1)求椭圆E的方程;
(2)若A,B分别为椭圆E的左、右顶点,动点M满足![]() ,且MA交椭圆E于点P.
,且MA交椭圆E于点P.
(i)求证:![]() 为定值;
为定值;
(ii)设PB与以PM为直径的圆的另一交点为Q,问:直线MQ是否过定点,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|2x+3|+|2x﹣1|.
(1)求不等式f(x)≤6的解集;
(2)若关于x的不等式f(x)<|m﹣1|的解集非空,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图①,利用斜二侧画法得到水平放置的![]() 的直观图
的直观图![]() ,其中
,其中![]() 轴,
轴,![]() 轴.若
轴.若![]() ,设
,设![]() 的面积为
的面积为![]() ,
,![]() 的面积为
的面积为![]() ,记
,记![]() ,执行如图②的框图,则输出
,执行如图②的框图,则输出![]() 的值
的值
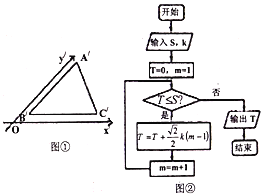
A. 12B. 10C. 9D. 6
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若数列{an}满足a1=1,a2=1,an+2=an+an+1,则称数列{an}为斐波那契数列,斐波那契螺旋线是根据斐波那契数列画出来的螺旋曲线,自然界中存在许多斐波那契螺旋线的图案,是自然界最完美的经典黄金比例.作图规则是在以斐波那契数为边的正方形拼成的长方形中画一个圆心角为90°的扇形,连起来的弧线就是斐波那契螺旋线,如图所示的7个正方形的边长分别为a1,a2,…,a7,在长方形ABCD内任取一点,则该点不在任何一个扇形内的概率为( )
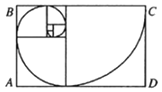
A.1![]() B.1
B.1![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com