练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    将1-9这9个不同的数字分别填入右图中的方格中，要求每行自左至右数字从小到大排，每列自上到下数字也从小到大排，并且5排在正中的方格，则不同的填法共有（ ）

    A．24种
    B．20种
    C．18种
    D．12种
    【答案】分析：根据题意，首先1、5、9一定是在左上斜的对角线上，安排2有两种情况，再安排3，也有两种但要分类：与2在一行或一列时，4有一种情况；与2不在一行或一列时，4有两种情况，在每种2，3，4确定的情况下，确定6，7，8，得到结果．
    解答：解：首先1、5、9一定是在左上斜的对角线上的
    安排2有两种情况，
    再安排3，也有两种但要分类：与2在一行或一列时，4有一种情况；
    与2不在一行或一列时，4有两种情况，
    在每种2，3，4确定的情况下，
    6，7，8均只有3中情况，
    故共2（1×1×3+1×2×3）=18
    故选C．
    点评：本题考查分步计数问题，解题时一定要分清做这件事需要分为几步，每一步包含几种方法，再根据分步乘法原理得到结果．本题是一个典型的排列组合的实际应用．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

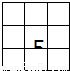
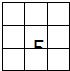    3、将1-9这9个不同的数字分别填入右图中的方格中，要求每行自左至右数字从小到大排，每列自上到下数字也从小到大排，并且5排在正中的方格，则不同的填法共有（　　）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    附加题（必做题）
    在0，1，2，3，…，9这十个自然数中，任取3个不同的数字．
    （1）求组成的三位数中是3的倍数的有多少个？
    （2）将取出的三个数字按从小到大的顺序排列，设ξ为三个数字中相邻自然数的组数（例如：若取出的三个数字为0，1，2，则相邻的组为0，1和1，2，此时ξ的值是2），求随机变量ξ的分布列及其数学期望Eξ．

    查看答案和解析>>

    科目：高中数学 来源：2012-2013学年黑龙江省齐齐哈尔市高三二模理科数学试卷（解析版） 题型：解答题

    （本小题满分12分）

    一个不透明的袋子中装有4个形状相同的小球，分别标有不同的数字2，3，4，，现从袋中随机摸出2个球，并计算摸出的这2个球上的数字之和，记录后将小球放回袋中搅匀，进行重复试验。记A事件为“数字之和为7”.试验数据如下表

    摸球总次数

    10

    20

    30

    60

    90

    120

    180

    240

    330

    450

    “和为7”出现的频数

    1

    9

    14

    24

    26

    37

    58

    82

    109

    150

    “和为7”出现的频率

    0.10

    0.45

    0.47

    0.40

    0.29

    0.31

    0.32

    0.34

    0.33

    0.33

    （参考数据：）

    （Ⅰ）如果试验继续下去，根据上表数据，出现“数字之和为7”的频率将稳定在它的概率附近。试估计“出现数字之和为7”的概率，并求的值；

    （Ⅱ）在（Ⅰ）的条件下，设定一种游戏规则：每次摸2球，若数字和为7，则可获得奖金7元，否则需交5元。某人摸球3次，设其获利金额为随机变量元，求的数学期望和方差。

     

    查看答案和解析>>

    科目：高中数学 来源： 题型：单选题

    将1-9这9个不同的数字分别填入右图中的方格中，要求每行自左至右数字从小到大排，每列自上到下数字也从小到大排，并且5排在正中的方格，则不同的填法共有


    1. A.
      24种
    2. B.
      20种
    3. C.
      18种
    4. D.
      12种

    查看答案和解析>>

    同步练习册答案