
【题目】如图,边长为3的等边三角形ABC,E,F分别在边AB,AC上,且![]() ,M为BC边的中点,AM交EF于点O,沿EF将
,M为BC边的中点,AM交EF于点O,沿EF将![]() ,折到DEF的位置,使
,折到DEF的位置,使![]() .
.
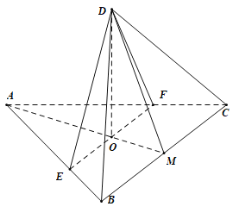
(1)证明![]() 平面EFCB;
平面EFCB;
(2)试在BC边上确定一点N,使![]() 平面DOC,并求
平面DOC,并求![]() 的值.
的值.
科目:高中数学 来源: 题型:
【题目】已知三棱锥P﹣ABC中,AC⊥BC,AC=BC=2,PA=PB=PC=3,O是AB中点,E是PB中点.
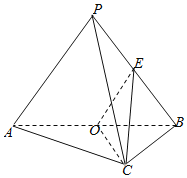
(1)证明:平面PAB⊥平面ABC;
(2)求点B到平面OEC的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() ,
,![]() 为自然对数的底数).
为自然对数的底数).
(1)若曲线![]() 在点
在点![]() 处的切线与直线
处的切线与直线![]() 垂直,求
垂直,求![]() 的单调区间;
的单调区间;
(2)若函数![]() 有两个极值点,求实数
有两个极值点,求实数![]() 的取值范围;
的取值范围;
(3)证明:当![]() 时,
时,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将函数f(x)=cos(2x![]() )的图象向左平移
)的图象向左平移![]() 个单位长度后,得到函数g(x)的图象,则下列结论中正确的是_____.(填所有正确结论的序号)
个单位长度后,得到函数g(x)的图象,则下列结论中正确的是_____.(填所有正确结论的序号)
①g(x)的最小正周期为4π;
②g(x)在区间[0,![]() ]上单调递减;
]上单调递减;
③g(x)图象的一条对称轴为x![]() ;
;
④g(x)图象的一个对称中心为(![]() ,0).
,0).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知四棱锥A-BCDE,其中AC=BC=2,AC⊥BC,CD//BE且CD=2BE,CD⊥平面ABC,F为AD的中点.
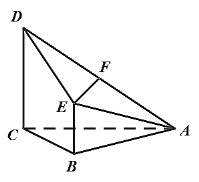
(1)求证:EF//平面ABC;
(2)设M是AB的中点,若DM与平面ABC所成角的正切值为![]() ,求平面ACD与平面ADE夹角的余弦值.
,求平面ACD与平面ADE夹角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设直线l的方程为(a﹣1)x+y+a+3=0,(a∈R).
(1)若直线l在两坐标轴上截距的绝对值相等,求直线l的方程;
(2)若直线l不经过第一象限,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“读书可以让人保持思想活跃,让人得到智慧启发,让人滋养浩然之气”,2018年第一期中国青年阅读指数数据显示,从供给的角度,文学阅读域是最多的,远远超过了其他阅读域的供给量.某校采用分层抽样的方法从1000名文科生和2000名理科生中抽取300名学生进行了在暑假阅读内容和阅读时间方面的调查,得到数据如表:
文学阅读人数 | 非文学阅读人数 | 调查人数 | |
理科生 | 130 | ||
文科生 | 45 | ||
合计 |
(1)先完成上面的表格,并判断能否有90%的把握认为学生所学文理与阅读内容有关?
(2从300名被调查的学生中,随机进取30名学生,整理其日平均阅读时间(单位:分钟)如表:
阅读时间 |
|
|
|
|
|
男生人数 | 2 | 4 | 3 | 5 | 2 |
女生人数 | 1 | 3 | 4 | 3 | 3 |
试估计这30名学生日阅读时间的平均值(同一组中的数据以这组数据所在区间中点的值作代表)
(3)从(2)中日均阅读时间不低于120分钟的学生中随机选取2人介绍阅读心得,求这两人都是女生的概率.
参考公式: 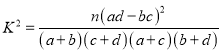 ,其中
,其中![]() .
.
参考数据:
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com