
【题目】已知函数![]() ,
,![]() ,
,![]() .
.
(1)讨论函数![]() 的单调性;
的单调性;
(2)若存在与函数![]() ,
,![]() 的图象都相切的直线,求
的图象都相切的直线,求![]() 的取值范围.
的取值范围.
【答案】(1)答案见解析;(2)![]() .
.
【解析】
(1)求![]() 的定义域,导数,利用二次函数的性质分类讨论导数的正负,从而求出
的定义域,导数,利用二次函数的性质分类讨论导数的正负,从而求出![]() 的单调性. (2)函数
的单调性. (2)函数![]() 的图象上点
的图象上点![]() 与函数
与函数![]() 的图象上点
的图象上点![]() 处切线相同,利用导数求切线的斜率建立关系式,求出导数和单调区间以及最值,运用单调性计算可求出
处切线相同,利用导数求切线的斜率建立关系式,求出导数和单调区间以及最值,运用单调性计算可求出![]() 的范围.
的范围.
(1)函数![]() 的定义域为
的定义域为![]() ,
,
![]() .
.
![]() ,
,
所以当![]() 即
即![]() 时,
时,![]() ,
,![]() 在
在![]() 上单调递增;
上单调递增;
当![]() ,即
,即![]() 或
或![]() 时,
时,
方程![]() 的根为
的根为![]() ,
,![]() .
.
当![]() 时,有
时,有![]() ,
,![]() ,
,![]() 在
在![]() 上单调递增;
上单调递增;
当![]() 时,有
时,有![]() .
.
|
|
|
|
| + | - | + |
| 增 | 减 | 增 |
综上:当![]() 时,
时,![]() 在
在![]() 上单调递增,
上单调递增,
当![]() 时,
时,![]() 在
在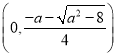 ,
,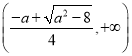 上单调递增,
上单调递增,
在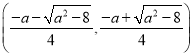 上单调递减.
上单调递减.
(2)设函数![]() 的图象上点
的图象上点![]() 与函数
与函数![]() 的图象上点
的图象上点![]() 处切线相同,
处切线相同,
则![]() ,
,
即![]() ,
,
由![]() 得
得![]() ①
①
由![]() ,
,
得![]() ②
②
由①②得:![]() ,
,
设![]()
问题转化为![]() 在
在![]() 有解,
有解,
则![]() ,
,
不妨设![]() ,
,
则当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,
,
∴![]() 在区间
在区间![]() 上单调递减,在区间
上单调递减,在区间![]() 上单调递增,
上单调递增,
∴![]() 是
是![]() 的最小值.
的最小值.
只需![]() ,即
,即![]() ③
③
而![]() ,故
,故![]() 代入③式,得
代入③式,得
![]() ,
,
令![]() ,易得
,易得![]() ,
,
![]() ,则
,则![]() 在
在![]() 递增.
递增.
故![]() 的解集是(0,1],即
的解集是(0,1],即![]() .
.
由![]() ,得
,得![]() .
.
即实数![]() 的取值范围是
的取值范围是![]() .
.


科目:高中数学 来源: 题型:
【题目】如图①,在等腰梯形![]() 中,
中,![]() ,
,![]() ,
,![]() .
.![]() ,交
,交![]() 于点
于点![]() .将
.将![]() 沿线段
沿线段![]() 折起,使得点
折起,使得点![]() 在平面
在平面![]() 内的投影恰好是点
内的投影恰好是点![]() ,如图.
,如图.
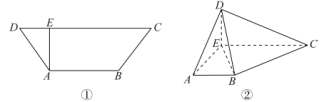
(1)若点![]() 为棱
为棱![]() 上任意一点,证明:平面
上任意一点,证明:平面![]() 平面
平面![]() .
.
(2)在棱![]() 上是否存在一点
上是否存在一点![]() ,使得三棱锥
,使得三棱锥![]() 的体积为
的体积为![]() ?若存在,确定
?若存在,确定![]() 点的位置;若不存在,请说明理由.
点的位置;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某城市为了解游客人数的变化规律,提高旅游服务质量,收集并整理了2017年1月至2019年12月期间月接待游客量(单位:万人)的数据,绘制了下面的折线图.根据该折线图,下列结论正确的是( )
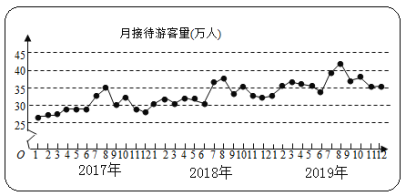
A.年接待游客量逐年增加
B.各年的月接待游客量高峰期大致在8月
C.2017年1月至12月月接待游客量的中位数为30
D.各年1月至6月的月接待游客量相对于7月至12月,波动性更小,变化比较平稳
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 、
、![]() 是抛物线
是抛物线![]() 上的两个不同的点,
上的两个不同的点,![]() 是坐标原点,若直线
是坐标原点,若直线![]() 与
与![]() 的斜率之积为
的斜率之积为![]() ,则下列结论正确的是( )
,则下列结论正确的是( )
A.![]()
B.以![]() 为直径的圆面积的最小值为
为直径的圆面积的最小值为![]()
C.直线![]() 过抛物线
过抛物线![]() 的焦点
的焦点
D.点![]() 到直线
到直线![]() 的距离不大于
的距离不大于![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校数学建模小组为了研究双层玻璃窗户中每层玻璃厚度![]() (每层玻璃的厚度相同)及两层玻璃间夹空气层厚度
(每层玻璃的厚度相同)及两层玻璃间夹空气层厚度![]() 对保温效果的影响,利用热传导定律得到热传导量
对保温效果的影响,利用热传导定律得到热传导量![]() 满足关系式
满足关系式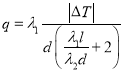 ,其中玻璃的热传导系数
,其中玻璃的热传导系数![]() 焦耳/(厘米·度),不流通、干燥空气的热传导系数
焦耳/(厘米·度),不流通、干燥空气的热传导系数![]() 焦耳/(厘米·度),
焦耳/(厘米·度),![]() 为室内外温度差,
为室内外温度差,![]() 值越小,保温效果越好,现有4种型号的双层玻璃窗户,具体数据如下表:
值越小,保温效果越好,现有4种型号的双层玻璃窗户,具体数据如下表:
型号 | 每层玻璃厚度 | 玻璃间夹空气层厚度 |
| 0.4 | 3 |
| 0.3 | 4 |
| 0.5 | 3 |
| 0.4 | 4 |
则保温效果最好的双层玻璃的型号是( )
A.![]() 型B.
型B.![]() 型C.
型C.![]() 型D.
型D.![]() 型
型
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,函数
,函数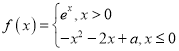 ,则下列说法正确的是( )
,则下列说法正确的是( )
A.若![]() ,则
,则![]() 的图象上存在唯一一对关于原点
的图象上存在唯一一对关于原点![]() 对称的点
对称的点
B.存在实数![]() 使得
使得![]() 的图象上存在两对关于原点
的图象上存在两对关于原点![]() 对称的点
对称的点
C.不存在实数![]() 使得
使得![]() 的图象上存在两对关于
的图象上存在两对关于![]() 轴对称的点
轴对称的点
D.若![]() 的图象上存在关于
的图象上存在关于![]() 轴对称的点,则
轴对称的点,则![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直四棱柱ABCD﹣A1B1C1D1中,底面ABCD是矩形,A1D与AD1交于点E,AA1=AD=2AB=4.
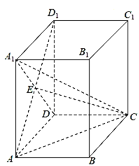
(1)证明:AE⊥平面ECD;
(2)求点C1到平面AEC的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
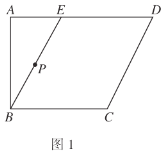
【题目】如图1,在四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 是
是![]() 上的点,
上的点,![]() ,
,![]() 为
为![]() 的中点.将
的中点.将![]() 沿
沿![]() 折起到
折起到![]() 的位置,使得
的位置,使得![]() ,如图2.
,如图2.
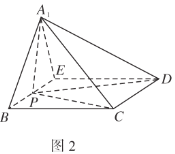
(1)求证:平面![]() 平面
平面![]() ;
;
(2)点![]() 在线段
在线段![]() 上,当直线
上,当直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() 时,求二面角
时,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在新冠病毒疫情爆发期间,口罩成为了个人的必需品.已知某药店有4种不同类型的口罩![]() ,
,![]() ,
,![]() ,
,![]() ,其中
,其中![]() 型口罩仅剩1只(其余3种库存足够).今甲、乙等5人先后在该药店各购买了1只口罩,统计发现他们恰好购买了3种不同类型的口罩,则所有可能的购买方式共有( )
型口罩仅剩1只(其余3种库存足够).今甲、乙等5人先后在该药店各购买了1只口罩,统计发现他们恰好购买了3种不同类型的口罩,则所有可能的购买方式共有( )
A.330种B.345种C.360种D.375种
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com