
【题目】如图,三棱锥P﹣ABC中,PA=PC,底面ABC为正三角形.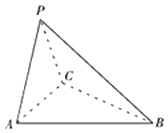
(Ⅰ)证明:AC⊥PB;
(Ⅱ)若平面PAC⊥平面ABC,AC=PC=2,求二面角A﹣PC﹣B的余弦值.
【答案】(Ⅰ)证明:如图,

取AC中点O,连接PO,BO,
∵PA=PC,∴PO⊥AC,
又∵底面ABC为正三角形,∴BO⊥AC,
∵PO∩OB=O,∴AC⊥平面POB,则AC⊥PB;
(Ⅱ)解:∵平面PAC⊥平面ABC,且平面PAC∩平面ABC=AC,
PO⊥AC,∴PO⊥平面ABC,
以O为原点,分别以OA、OB、OP所在直线为x、y、z轴建立空间直角坐标系,
∵AC=PC=2,∴P(0,0, ![]() ),B(0,
),B(0, ![]() ,0),C(﹣1,0,0),
,0),C(﹣1,0,0), ![]() ,
,
![]() ,
,
设平面PBC的一个法向量为 ![]() ,
,
由  ,取y=﹣1,得
,取y=﹣1,得 ![]() ,
,
又 ![]() 是平面PAC的一个法向量,
是平面PAC的一个法向量,
∴cos< ![]() >=
>= ![]() .
.
∴二面角A﹣PC﹣B的余弦值为 ![]() .
.
【解析】(1)取AC中点O,连接PO,BO,根据等腰三角形三线合一得出PO⊥AC,再由ABC为正三角形BO⊥AC,从而得到AC⊥平面POB,则AC⊥PB,(2)以O为原点,分别以OA、OB、OP所在直线为x、y、z轴建立空间直角坐标系,用法向量法求出二面角的余弦值.
【考点精析】掌握空间中直线与直线之间的位置关系是解答本题的根本,需要知道相交直线:同一平面内,有且只有一个公共点;平行直线:同一平面内,没有公共点;异面直线: 不同在任何一个平面内,没有公共点.


科目:高中数学 来源: 题型:
【题目】某工艺品厂要设计一个如图1所示的工艺品,现有某种型号的长方形材料如图2所示,其周长为4m,这种材料沿其对角线折叠后就出现图1的情况.如图,ABCD(AB>AD)为长方形的材料,沿AC折叠后AB'交DC于点P,设△ADP的面积为S2 , 折叠后重合部分△ACP的面积为S1 .
(Ⅰ)设AB=xm,用x表示图中DP的长度,并写出x的取值范围;
(Ⅱ)求面积S2最大时,应怎样设计材料的长和宽?
(Ⅲ)求面积(S1+2S2)最大时,应怎样设计材料的长和宽?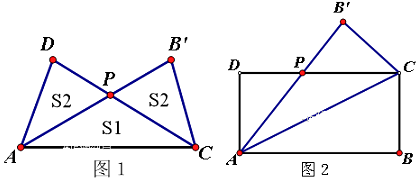
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在四棱锥P﹣ABCD中,底面ABCD是∠DAB=60°且边长为a的菱形,侧面PAD为正三角形,其所在平面垂直于底面ABCD,若G为AD边的中点, 
(1)求证:BG⊥平面PAD;
(2)求证:AD⊥PB;
(3)若E为BC边的中点,能否在棱PC上找到一点F,使平面DEF⊥平面ABCD,并证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在边长为2的正六边形ABCDEF中,动圆Q的半径为1,圆心在线段CD(含端点)上运动,P是圆Q上及内部的动点,设向量 ![]() (m,n为实数),则m+n的取值范围是( )
(m,n为实数),则m+n的取值范围是( )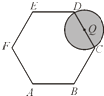
A.(1,2]
B.[5,6]
C.[2,5]
D.[3,5]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线C的极坐标方程是ρ=2,以极点为原点,极轴为x轴的正半轴建立平面直角坐标系,直线l的参数方程为 ![]() (t为参数).
(t为参数).
(Ⅰ)写出直线l的普通方程与曲线C的直角坐标方程;
(Ⅱ)设曲线C经过伸缩变换 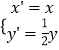 得到曲线C',若点P(1,0),直线l与C'交与A,B,求|PA||PB|,|PA|+|PB|.
得到曲线C',若点P(1,0),直线l与C'交与A,B,求|PA||PB|,|PA|+|PB|.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图中的三个直角三角形是一个体积为20cm3的几何体的三视图,则该几何体外接球的面积(单位:cm2)等于( )
A.55π
B.75π
C.77π
D.65π
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C的中心在坐标原点,焦点在x轴上,左顶点为A,左焦点为F1(﹣2,0),点B(2, ![]() )在椭圆C上,直线y=kx(k≠0)与椭圆C交于E,F两点,直线AE,AF分别与y轴交于点M,N
)在椭圆C上,直线y=kx(k≠0)与椭圆C交于E,F两点,直线AE,AF分别与y轴交于点M,N
(Ⅰ)求椭圆C的方程;
(Ⅱ)在x轴上是否存在点P,使得无论非零实数k怎样变化,总有∠MPN为直角?若存在,求出点P的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=(log2x﹣2)(log4x﹣ ![]() )
)
(1)当x∈[2,4]时.求该函数的值域;
(2)若f(x)≥mlog2x对于x∈[4,16]恒成立,求m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知△ABC的内角A,B,C所对的边分别为a,b,c且a+2c=2bcosA.
(1)求角B的大小;
(2)若b=2 ![]() ,a+c=4,求△ABC的面积.
,a+c=4,求△ABC的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com