
【题目】正三棱柱ABC﹣A1B1C1的棱长都为2,E,F,G为 AB,AA1 , A1C1的中点,则B1F 与面GEF成角的正弦值( )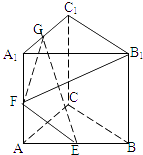
A.![]()
B.![]()
C.![]()
D.![]()
【答案】A
【解析】解:取A1B1中点M,连接EM,则EM∥AA1 , EM⊥平面ABC,连接GM
∵G为A1C1的中点,棱长为
∴GM= ![]() B1C1=1,A1G═A1F=1,FG=
B1C1=1,A1G═A1F=1,FG= ![]() ,FE=
,FE= ![]() ,GE=
,GE= ![]()
在平面EFG上作FN⊥GE,则∵△GFE是等腰三角形,∴FN= ![]() ,
,
∴S△GEF= ![]() GE×FN=
GE×FN= ![]() ,
,
S△EFB1=S正方形ABB1A1﹣S△A1B1F﹣S△BB1E﹣S△AFE= ![]() ,
,
作GH⊥A1B1 , GH= ![]() ,
,
∴V三棱锥G﹣FEB1= ![]() S△EFB1×GH=
S△EFB1×GH= ![]() ,
,
设B1到平面EFG距离为h,则V三棱锥B1﹣EFG= ![]() S△GEF=
S△GEF= ![]() ,
,
∵V三棱锥G﹣FEB1=V三棱锥B1﹣EFG ,
∴ ![]() ,
,
∴h= ![]()
设B1F与平面GEF成角为θ,
∵B1F= ![]()
∴sinθ= ![]() =
= ![]()
∴B1F与面GEF所成的角的正弦值为 ![]() .
.
故选A.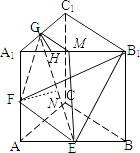
【考点精析】利用空间角的异面直线所成的角对题目进行判断即可得到答案,需要熟知已知![]() 为两异面直线,A,C与B,D分别是
为两异面直线,A,C与B,D分别是![]() 上的任意两点,
上的任意两点,![]() 所成的角为
所成的角为![]() ,则
,则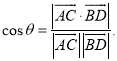 .
.


 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案科目:高中数学 来源: 题型:
【题目】已知{an}是等差数列,满足a1=3,a4=12,数列{bn}满足b1=4,b4=20,且{bn﹣an}为等比数列.
(1)求数列{an}和{bn}的通项公式;
(2)求数列{bn}的前n项和.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点A(6,2),B(3,2),动点M满足|MA|=2|MB|.
(1)求点M的轨迹方程;
(2)设M的轨迹与y轴的交点为P,过P作斜率为k的直线l与M的轨迹交于另一点Q,若C(1,2k+2),求△CPQ面积的最大值,并求出此时直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若直线 l1和l2 是异面直线,l1在平面 α内,l2在平面β内,l是平面α与平面β的交线,则下列命题正确的是( )
A.l与l1 , l2都不相交
B.l与l1 , l2都相交
C.l至多与l1 , l2中的一条相交
D.l至少与l1 , l2中的一条相交
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的焦点
的焦点![]() 也是椭圆
也是椭圆![]() 的一个焦点,
的一个焦点,![]() 与
与![]() 的公共弦的长为
的公共弦的长为![]() .
.
(1)求![]() 的方程;
的方程;
(2)过点![]() 的直线
的直线![]() 与
与![]() 相交于
相交于![]() ,
,![]() 两点,与
两点,与![]() 相交于
相交于![]() ,
,![]() 两点,且
两点,且![]() 与
与![]() 同向
同向
(ⅰ)若![]() ,求直线
,求直线![]() 的斜率
的斜率
(ⅱ)设![]() 在点
在点![]() 处的切线与
处的切线与![]() 轴的交点为
轴的交点为![]() ,证明:直线
,证明:直线![]() 绕点
绕点![]() 旋转时,
旋转时,![]() 总是钝角三角形
总是钝角三角形
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图为一简单组合体,其底面ABCD为正方形,棱PD与EC均垂直于底面ABCD,PD=2EC,N为PB的中点,求证: 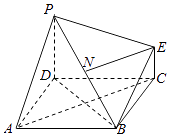
(1)平面EBC∥平面PDA;
(2)NE⊥平面PDB.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知单调递增的等比数列{an}满足:a2+a3+a4=28,且a3+2是a2 , a4的等差中项.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)设bn=anlog ![]() an , 求数列{bn}的前n项和Sn .
an , 求数列{bn}的前n项和Sn .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com