
【题目】某公司生产一种产品,从流水线上随机抽取100件产品,统计其质量指数并绘制频率分布直方图(如图1):
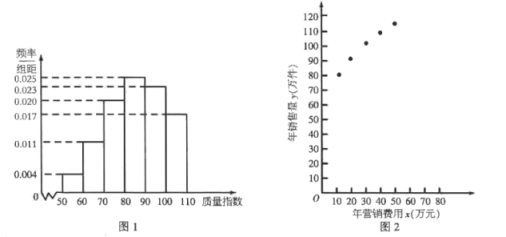
产品的质量指数在![]() 的为三等品,在
的为三等品,在![]() 的为二等品,在
的为二等品,在![]() 的为一等品,该产品的三、二、一等品的销售利润分别为每件1.5,3.5,5.5(单位:元),以这100件产品的质量指数位于各区间的频率代替产品的质量指数位于该区间的概率.
的为一等品,该产品的三、二、一等品的销售利润分别为每件1.5,3.5,5.5(单位:元),以这100件产品的质量指数位于各区间的频率代替产品的质量指数位于该区间的概率.
(1)求每件产品的平均销售利润;
(2)该公司为了解年营销费用![]() (单位:万元)对年销售量
(单位:万元)对年销售量![]() (单位:万件)的影响,对近5年的年营销费用
(单位:万件)的影响,对近5年的年营销费用![]() 和年销售量
和年销售量![]()
![]() 数据做了初步处理,得到的散点图(如图2)及一些统计量的值.
数据做了初步处理,得到的散点图(如图2)及一些统计量的值.
|
|
|
|
16.30 | 24.87 | 0.41 | 1.64 |
表中![]() ,
,![]() ,
,![]() ,
,![]()
根据散点图判断,![]() 可以作为年销售量
可以作为年销售量![]() (万件)关于年营销费用
(万件)关于年营销费用![]() (万元)的回归方程.
(万元)的回归方程.
(ⅰ)建立![]() 关于
关于![]() 的回归方程;
的回归方程;
(ⅱ)用所求的回归方程估计该公司应投入多少营销费,才能使得该产品一年的收益达到最大?(收益=销售利润-营销费用,取![]() )
)
参考公式:对于一组数据:![]() ,
,![]() ,
,![]() ,
,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小乘估计分别为
的斜率和截距的最小乘估计分别为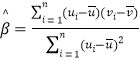 ,
,![]()
【答案】(1) 平均销售利润为4元.
(2) (ⅰ)![]() (ⅱ)投入256万元营销费,能使得该产品一年的收益达到最大768万元
(ⅱ)投入256万元营销费,能使得该产品一年的收益达到最大768万元
【解析】
(1) 设每件产品的销售利润为![]() 元,则
元,则![]() 的所有可能取值为1.5,3.5,5.5,求出相应的概率值,得到分布列与期望值;
的所有可能取值为1.5,3.5,5.5,求出相应的概率值,得到分布列与期望值;
(2) (ⅰ)由![]() 得,
得,![]() ,令
,令![]() ,
,![]() ,
,![]() ,则
,则![]() ,利用表中数据求出
,利用表中数据求出![]() 即可;(ⅱ)设年收益为
即可;(ⅱ)设年收益为![]() 万元,则
万元,则![]() ,利用导函数即可得到结果.
,利用导函数即可得到结果.
(1)设每件产品的销售利润为![]() 元,则
元,则![]() 的所有可能取值为1.5,3.5,5.5
的所有可能取值为1.5,3.5,5.5
由直方图可得:一、二、三等品的频率分别为0.4,0.45,0.15,
所以![]() ,
,
![]() ,
,
![]() ,
,
所以:随机变量![]() 的分布列为:
的分布列为:
| 1.5 | 3.5 | 5.5 |
P | 0.15 | 0.45 | 0.4 |
所以,![]()
故每件产品的平均销售利润为4元.
(2)(ⅰ)由![]() 得,
得,![]() ,
,
令![]() ,
,![]() ,
,![]() ,则
,则![]() ,
,
由表中数据可得,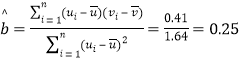 ,
,
则![]()
所以,![]() ,即
,即![]()
因为![]() ,所以
,所以![]()
故所求的回归方程为![]()
(ⅱ)设年收益为![]() 万元,则
万元,则![]()
设![]() ,
,![]() ,则
,则![]()
当![]() 时,
时,![]() ,
,![]() 在
在![]() 单调递增,
单调递增,
当![]() 时,
时,![]() ,
,![]() 在
在![]() 单调递减.
单调递减.
所以,当![]() ,即
,即![]() 时,
时,![]() 有最大值为768
有最大值为768
即该厂应投入256万元营销费,能使得该产品一年的收益达到最大768万元.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】甲、乙两人参加某种选拔测试,在备选的10道题中,甲答对其中每道题的概率都是![]() ,乙能答对其中的5道题。规定每次考试都从备选的10道题中随机抽出3道题进行测试,答对一题加10分,答错一题(不答视为答错)减5分,至少得15分才能入选.
,乙能答对其中的5道题。规定每次考试都从备选的10道题中随机抽出3道题进行测试,答对一题加10分,答错一题(不答视为答错)减5分,至少得15分才能入选.
(I)求甲能入选的概率.
(II)求乙得分的分布列和数学期望;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】圆周率是圆的周长与直径的比值,一般用希腊字母![]() 表示,早在公元480年左右,南北朝时期的数学家祖冲之就得出精确到小数点后7位的结果,他是世界上第一个把圆周率的数值计算到小数点后第七位的人,这比欧洲早了约1000年,在生活中,我们也可以通过设计下面的实验来估计
表示,早在公元480年左右,南北朝时期的数学家祖冲之就得出精确到小数点后7位的结果,他是世界上第一个把圆周率的数值计算到小数点后第七位的人,这比欧洲早了约1000年,在生活中,我们也可以通过设计下面的实验来估计![]() 的值;从区间
的值;从区间![]() 内随机抽取200个数,构成100个数对
内随机抽取200个数,构成100个数对![]() ,其中满足不等式
,其中满足不等式![]() 的数对
的数对![]() 共有11个,则用随机模拟的方法得到的
共有11个,则用随机模拟的方法得到的![]() 的近似值为( )
的近似值为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥P﹣ABC中,E,F分别为AC,BC的中点.
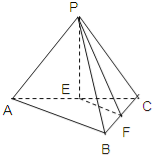
(1)求证:EF∥平面PAB;
(2)若平面PAC⊥平面ABC,且PA=PC,∠ABC=90°,求证:平面PEF⊥平面PBC.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】自2017年,大连“蜗享出行”正式引领共享汽车,改变人们传统的出行理念,给市民出行带来了诸多便利![]() 该公司购买了一批汽车投放到市场给市民使用
该公司购买了一批汽车投放到市场给市民使用![]() 据市场分析,每辆汽车的营运累计收入
据市场分析,每辆汽车的营运累计收入![]() 单位:元
单位:元![]() 与营运天数
与营运天数![]() 满足
满足![]() .
.
![]() 要使营运累计收入高于1400元求营运天数的取值范围;
要使营运累计收入高于1400元求营运天数的取值范围;
![]() 每辆汽车营运多少天时,才能使每天的平均营运收入最大?
每辆汽车营运多少天时,才能使每天的平均营运收入最大?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com