考点:数列与不等式的综合,等差数列与等比数列的综合
专题:等差数列与等比数列
分析:(1)由题意联立方程组,由此求出等差数列的首项和公差,从而能够求出数列{a
n}的通项公式.
(2)由(1)可得b
n=
=
=
(
-),T
n=
(1
-+-+…+-)=
(1
-)=
,
a
n+1≥λT
n,对任意正整数n都成立,即-
≥λ•
对任意正整数n都成立,即λ≤-
,对任意正整数n都成立,令f(n)=-
,利用导数求出函数的最小值,即可得出结论.
解答:
解:(1)S
5=3a
5-2,所以5a
1+
=3(a
1+4d)-2.①
因为a
1,a
2,a
5成等比数列,所以a
1(a
1+4d)=
(a1+d)2.②
由①,②及d≠0可得:a
1=1,d=2.
所以a
n=1+2(n-1)=2n-1.
(2)b
n=
=
=
(
-),
∴T
n=
(1
-+-+…+-)=
(1
-)=
,
∵a
n+1≥λT
n,对任意正整数n都成立,
即2n+1≥λ•
对任意正整数n都成立,
即λ≤
,对任意正整数n都成立,
令f(n)=
,则f
′(n)=8-
>0,
∴f(n)≥f(1)=9,
∴λ≤9.
∴实数λ的取值范围是(-∞,9].
点评:本题考查等差数列的通项公式和前n项和公式的应用,考查恒成立问题的等价转化思想的运用能力.解题时要认真审题,仔细解答,注意合理地进行等价转化.属于中档题.



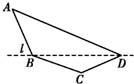 某单位设计一个展览沙盘,现欲在沙盘平面内,铺设一个对角线在L上的四边形电气线路,如图所示.为充分利用现有材料,边BC,CD用一根5米长的材料弯折而成,边BA,AD用一根9米长的材料弯折而成,使A+C=180°,且AB=BC.设AB=x米,cos A=f(x).
某单位设计一个展览沙盘,现欲在沙盘平面内,铺设一个对角线在L上的四边形电气线路,如图所示.为充分利用现有材料,边BC,CD用一根5米长的材料弯折而成,边BA,AD用一根9米长的材料弯折而成,使A+C=180°,且AB=BC.设AB=x米,cos A=f(x).