
【题目】若[x]表示不超过x的最大整数,则[lg2]+[lg3]+…+lg[2017]+[lg ![]() ]+[lg
]+[lg ![]() ]+…+[lg
]+…+[lg ![]() ]= .
]= .
【答案】-2013
【解析】解:当2≤n≤9时,[lgn]=0,
当10≤n≤99时,[lgn]=1,
当100≤n≤999时,[lgn]=2,
当1000≤n≤9999时,[lgn]=3,
故[lg2]+[lg3]+…+[lg2016]+[2017]
=0×8+1×90+2×900+3×1018
=90+1800+3054
=4944;
当 ![]() ≤
≤ ![]() ≤
≤ ![]() ,[lg
,[lg ![]() ]=﹣1;
]=﹣1;
当 ![]() ≤
≤ ![]() ≤
≤ ![]() 时,[lg
时,[lg ![]() ]=﹣2;
]=﹣2;
当 ![]() ≤
≤ ![]() ≤
≤ ![]() 时,[lg
时,[lg ![]() ]=﹣3;
]=﹣3;
当 ![]() ≤
≤ ![]() ≤
≤ ![]() 时,[lg
时,[lg ![]() ]=﹣4.
]=﹣4.
则[lg ![]() ]+[lg
]+[lg ![]() ]+…+[lg
]+…+[lg ![]() ]
]
=(﹣1)×9+(﹣2)×90+(﹣3)×900+(﹣4)×1017
=﹣6957,
故原式=4944﹣6957=﹣2013.
所以答案是:﹣2013.
【考点精析】认真审题,首先需要了解数列的前n项和(数列{an}的前n项和sn与通项an的关系 ).
).


科目:高中数学 来源: 题型:
【题目】若在定义域内存在实数x0使得f(x0+1)=f(x0)+f(1)成立则称函数f(x)有“溜点x0”
(1)若函数 ![]() 在(0,1)上有“溜点”,求实数m的取值范围;
在(0,1)上有“溜点”,求实数m的取值范围;
(2)若函数f(x)=lg( ![]() )在(0,1)上有“溜点”,求实数a的取值范围.
)在(0,1)上有“溜点”,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为比较甲,乙两地某月14时的气温,随机选取该月中的5天,将这5天中14时的气温数据(单位:℃)制成如图所示的茎叶图,考虑以下结论:
①甲地该月14时的平均气温低于乙地该月14时的平均气温;
②甲地该月14时的平均气温高于乙地该月14时的平均气温;
③甲地该月14时的气温的标准差小于乙地该月14时的气温的标准差;
④甲地该月14时的气温的标准差大于乙地该月14时的气温的标准差.
其中根据茎叶图能得到的统计结论的编号为( )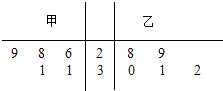
A.①③
B.①④
C.②③
D.②④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图为四棱锥P﹣ABCD的表面展开图,四边形ABCD为矩形, ![]() ,AD=1.已知顶点P在底面ABCD上的射影为点A,四棱锥的高为
,AD=1.已知顶点P在底面ABCD上的射影为点A,四棱锥的高为 ![]() ,则在四棱锥P﹣ABCD中,PC与平面ABCD所成角的正切值为 .
,则在四棱锥P﹣ABCD中,PC与平面ABCD所成角的正切值为 . 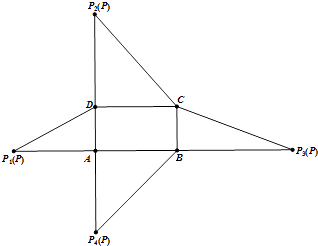
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,PA⊥底面ABCD,底面ABCD为直角梯形,AD∥BC,∠BAD=90°,PA=AD=AB=2BC=2,过AD的平面分别交PB,PC于M,N两点. 
(1)求证:MN∥BC;
(2)若M,N分别为PB,PC的中点,
①求证:PB⊥DN;
②求二面角P﹣DN﹣A的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥A﹣BCDE中,底面BCDE为矩形,侧面ABC⊥底面BCDE,BC=2,CD= ![]() ,AB=AC.
,AB=AC. 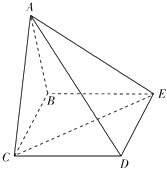
(1)证明:AD⊥CE;
(2)设CE与平面ABE所成的角为45°,求二面角C﹣AD﹣E的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2014年“五一节”期间,高速公路车辆较多,交警部门通过路面监控装置抽样调查某一山区路段汽车行驶速度,采用的方法是:按到达监控点先后顺序,每隔50辆抽取一辆,总共抽取120辆,分别记下其行车速度,将行车速度(km/h)分成七段[60,65),[65,70),[70,75),[75,80),[80,85),[85,90),[90,95)后得到如图所示的频率分布直方图,据图解答下列问题: 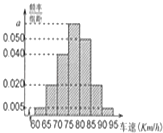
(1)求a的值,并说明交警部门采用的是什么抽样方法?
(2)求这120辆车行驶速度的众数和中位数的估计值(精确到0.1);
(3)若该路段的车速达到或超过90km/h即视为超速行驶,试根据样本估计该路段车辆超速行驶的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com