(Ⅰ)解:因为f(x)为奇函数,所以f(-x)=-f(x),所以b=d=0,
所以f(x)=ax
3+cx,求导函数,可得f′(x)=3ax
2+c
由f'(1)=0,得3a+c=0,由
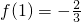
,得
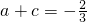
解之得:
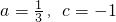
从而,函数解析式为:
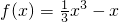
(Ⅱ)证明:由于f'(x)=x
2-1,设任意两数x
1,x
2∈[-1,1]是函数f(x)图象上两点的横坐标,则这两点的切线的斜率分别是:
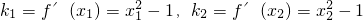
又因为-1≤x
1≤1,-1≤x
2≤1,所以k
1≤0,k
2≤0,得:k
1k
2≥0,知k
1k
2≠-1
故当x∈[-1,1]时,函数f(x)图象上任意两点的切线不可能垂直
(Ⅲ)解:|f(2sinα)-f(2sinβ)|≤m恒成立,等价于|f(x)|
max-|f(x)|
min≤m
由于-2≤2sinα≤2,-2≤2sinβ≤2,∴只需求出
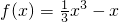
在[-2,2]上的最值
而f'(x)=x
2-1,由f'(x)=0解得x=±1
列表如下:
| x | -2 | (-2,-1) | -1 | (-1,1) | 1 | (1,2) | 2 |
| f'(x) | | + | 0 | - | 0 | + | |
| f(x) |  | 递增 |  | 递减 |  | 递增 |  |
∴
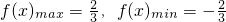
,
∴

,
∴m的最小值为

.
分析:(Ⅰ)根据f(x)为奇函数,可得b=d=0,求导函数,利用f'(1)=0,
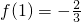
,即可求得函数解析式;
(Ⅱ)设任意两数x
1,x
2∈[-1,1]是函数f(x)图象上两点的横坐标,求出这两点的切线的斜率,证明斜率之积k
1k
2≠-1即可;
(Ⅲ)|f(2sinα)-f(2sinβ)|≤m恒成立,等价于|f(x)|
max-|f(x)|
min≤m,由于-2≤2sinα≤2,-2≤2sinβ≤2,只需求出
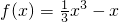
在[-2,2]上的最值,即可求得m的最小值.
点评:本题考查导数知识的运用,考查导数的几何意义,考查恒成立问题,解题的关键是将|f(2sinα)-f(2sinβ)|≤m恒成立,转化为|f(x)|
max-|f(x)|
min≤m.

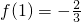 .
.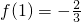 ,得
,得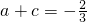
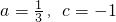
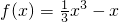
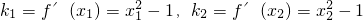
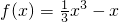 在[-2,2]上的最值
在[-2,2]上的最值



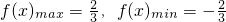 ,
, ,
, .
.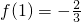 ,即可求得函数解析式;
,即可求得函数解析式;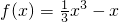 在[-2,2]上的最值,即可求得m的最小值.
在[-2,2]上的最值,即可求得m的最小值.
