
【题目】已知离心率为![]() 的椭圆
的椭圆![]() 经过抛物线
经过抛物线![]() 的焦点
的焦点![]() ,斜率为1的直线
,斜率为1的直线![]() 经过
经过![]() 且与椭圆交于
且与椭圆交于![]() 两点.
两点.
(1)求![]() 面积;
面积;
(2)动直线![]() 与椭圆有且仅有一个交点,且与直线
与椭圆有且仅有一个交点,且与直线![]() 分别交于
分别交于![]() 两点,
两点,![]() 为椭圆的右焦点,证明
为椭圆的右焦点,证明![]() 为定值.
为定值.
科目:高中数学 来源: 题型:
【题目】为了贯彻落实党中央精准扶贫决策,某市将其低收入家庭的基本情况经过统计绘制如图,其中各项统计不重复.若该市老年低收入家庭共有900户,则下列说法错误的是( )

A.该市总有 15000 户低收入家庭
B.在该市从业人员中,低收入家庭共有1800户
C.在该市无业人员中,低收入家庭有4350户
D.在该市大于18岁在读学生中,低收入家庭有 800 户
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,在等腰梯形![]() 中,两腰
中,两腰![]() ,底边
,底边![]() 是
是![]() 的三等分点,
的三等分点,![]() 是
是![]() 的中点.分别沿
的中点.分别沿![]() 将四边形
将四边形![]() 和
和![]() 折起,使
折起,使![]() 重合于点
重合于点![]() ,得到如图2所示的几何体.在图2中,
,得到如图2所示的几何体.在图2中,![]() 分别为
分别为![]() 的中点.
的中点.
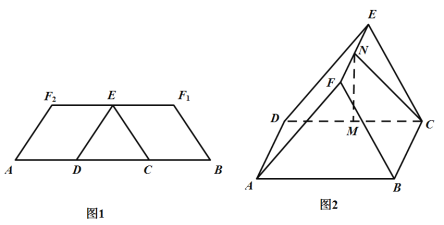
(1)证明:![]() 平面
平面![]()
(2)求几何体![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,在等腰梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 为
为![]() 的中点.现分别沿
的中点.现分别沿![]() ,
,![]() 将
将![]() 和
和![]() 折起,点
折起,点![]() 折至点
折至点![]() ,点
,点![]() 折至点
折至点![]() ,使得平面
,使得平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,连接
,连接![]() ,如图2.
,如图2.

(Ⅰ)若![]() 、
、![]() 分别为
分别为![]() 、
、![]() 的中点,求证:平面
的中点,求证:平面![]() 平面
平面![]() ;
;
(Ⅱ)求多面体![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,在等腰梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 为
为![]() 的中点.现分别沿
的中点.现分别沿![]() ,
,![]() 将
将![]() 和
和![]() 折起,点
折起,点![]() 折至点
折至点![]() ,点
,点![]() 折至点
折至点![]() ,使得平面
,使得平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,连接
,连接![]() ,如图2.
,如图2.

(Ⅰ)若平面![]() 内的动点
内的动点![]() 满足
满足![]() 平面
平面![]() ,作出点
,作出点![]() 的轨迹并证明;
的轨迹并证明;
(Ⅱ)求平面![]() 与平面
与平面![]() 所成锐二面角的余弦值.
所成锐二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为推动实施健康中国战略,树立国家大卫生、大健康概念,手机APP也推出了多款健康运动软件,如“微信运动”,杨老师的微信朋友圈内有![]() 位好友参与了“微信运动”,他随机选取了
位好友参与了“微信运动”,他随机选取了![]() 位微信好友(女
位微信好友(女![]() 人,男
人,男![]() 人),统计其在某一天的走路步数,其中,女性好友的走路步数数据记录如下:
人),统计其在某一天的走路步数,其中,女性好友的走路步数数据记录如下:
5860 | 8520 | 7326 | 6798 | 7325 | 8430 | 3216 | 7453 | 11754 | 9860 |
8753 | 6450 | 7290 | 4850 | 10223 | 9763 | 7988 | 9176 | 6421 | 5980 |
男性好友走路的步数情况可分为五个类别:![]() 步(说明“
步(说明“![]() ”表示大于等于
”表示大于等于![]() ,小于等于
,小于等于![]() ,下同),
,下同),![]() 步,
步,![]() 步,
步,![]() 步及以上,且
步及以上,且![]() 三种类别人数比例为
三种类别人数比例为![]() ,将统计结果绘制如图所示的条形图,若某人一天的走路步数超过
,将统计结果绘制如图所示的条形图,若某人一天的走路步数超过![]() 步被系统认定为“卫健型”,否则被系统认定为“进步型”.
步被系统认定为“卫健型”,否则被系统认定为“进步型”.
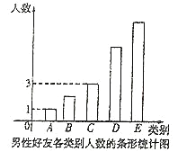
(1)若以杨老师选取的好友当天行走步数的频率分布来估计所有微信好友每日走路步数的概率分布,请估计杨老师的微信好友圈里参与“微信运动”的![]() 名好友中,每天走路步数在
名好友中,每天走路步数在![]() 步的人数;
步的人数;
(2)请根据选取的样本数据完成下面的![]() 列联表并据此判断能否有
列联表并据此判断能否有![]() 以上的把握认定“认定类型”与“性别”有关?
以上的把握认定“认定类型”与“性别”有关?
卫健型 | 进步型 | 总计 | |
男 | 20 | ||
女 | 20 | ||
总计 | 40 |
附: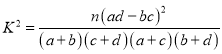 ,
,
| 0.10 | 0.05 | 0.025 | 0.010 |
| 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程:在平面直角坐标系![]() 中,曲线
中,曲线![]() :
:![]() (
(![]() 为参数),在以平面直角坐标系的原点为极点、
为参数),在以平面直角坐标系的原点为极点、![]() 轴的正半轴为极轴,且与平面直角坐标系
轴的正半轴为极轴,且与平面直角坐标系![]() 取相同单位长度的极坐标系中,曲线
取相同单位长度的极坐标系中,曲线![]() :
:![]() .
.
(1)求曲线![]() 的普通方程以及曲线
的普通方程以及曲线![]() 的平面直角坐标方程;
的平面直角坐标方程;
(2)若曲线![]() 上恰好存在三个不同的点到曲线
上恰好存在三个不同的点到曲线![]() 的距离相等,求这三个点的极坐标.
的距离相等,求这三个点的极坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com