
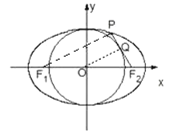
【题目】已知![]() 是椭圆
是椭圆![]() 的左、右顶点,
的左、右顶点,![]() 为椭圆
为椭圆![]() 的左、右焦点,点
的左、右焦点,点![]() 为椭圆
为椭圆![]() 上一点(
上一点(![]() 点在第一象限),线段
点在第一象限),线段![]() 与圆
与圆![]() 相切于点
相切于点![]() ,且点
,且点![]() 为线段
为线段![]() 的中点.
的中点.
(1)求线段![]() 的长;
的长;
(2)求椭圆![]() 的离心率;
的离心率;
(3)设直线![]() 交椭圆于
交椭圆于![]() 两点(其中点
两点(其中点![]() 在第一象限),过点
在第一象限),过点![]() 作
作![]() 的平行线
的平行线![]() 交椭圆
交椭圆![]() 于点
于点![]() ,
,![]() 交
交![]() 于点
于点![]() ,求
,求![]() .
.
【答案】(1)2b; (2)![]() ; (3)
; (3)![]() .
.
【解析】
(1)由OQ为△![]() 的中位线,直接得解;
的中位线,直接得解;
(2)由椭圆的定义结合直角三角形的勾股数建立a,b的方程,解得a,b的关系,从而可得离心率.
(3)由(2)可知![]() 及椭圆方程可设为
及椭圆方程可设为![]() ,(t>0),联立直线OQ的方程与椭圆方程求得M、N坐标,再联立
,(t>0),联立直线OQ的方程与椭圆方程求得M、N坐标,再联立![]() 的方程与椭圆方程得到D坐标,从而可得直线BD的方程,再与直线OQ的方程联立,解得
的方程与椭圆方程得到D坐标,从而可得直线BD的方程,再与直线OQ的方程联立,解得![]() ,利用面积比转化为线段比可得结果.
,利用面积比转化为线段比可得结果.
(1)连接OQ,![]() ,如图,OQ为△
,如图,OQ为△![]() 的中位线,由题意知OQ=b,则
的中位线,由题意知OQ=b,则![]() =2b.
=2b.
(2)由椭圆的定义结合(1)可得![]() ,
,![]() ,
,
则![]() ,得
,得![]() ,解得
,解得![]() ,
,
则![]() ,故椭圆的离心率为
,故椭圆的离心率为![]() .
.
(3)由(2)可知![]() ,设直线OQ的方程为x=2y,椭圆方程设为
,设直线OQ的方程为x=2y,椭圆方程设为![]() ,(t>0),
,(t>0),
由![]() 得25y2=
得25y2=![]() ,得到
,得到![]() ,
,![]() ,
,
又点![]() 作
作![]() 的平行线
的平行线![]() 的方程设为x=2y-3t,
的方程设为x=2y-3t,
由![]() 得4(2y-3t)2
得4(2y-3t)2![]() =
=![]() ,即25
,即25![]() -48ty=0,
-48ty=0,
解得y=0或y=![]() ,即D(
,即D(![]() ),又B(3t,0)
),又B(3t,0)
∴直线BD的方程为y=![]() ,与
,与![]() 联立,解得
联立,解得![]() ,
,
由三角形的面积公式得![]() =
=![]() =
=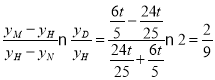 .
.


科目:高中数学 来源: 题型:
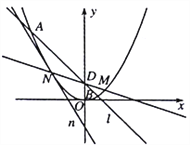
【题目】如图,在平面直角坐标系![]() 中,点
中,点![]() 在抛物线
在抛物线![]() :
: ![]() 上,直线
上,直线![]() :
: ![]() 与抛物线
与抛物线![]() 交于
交于![]() ,
, ![]() 两点,且直线
两点,且直线![]() ,
, ![]() 的斜率之和为-1.
的斜率之和为-1.
(1)求![]() 和
和![]() 的值;
的值;
(2)若![]() ,设直线
,设直线![]() 与
与![]() 轴交于
轴交于![]() 点,延长
点,延长![]() 与抛物线
与抛物线![]() 交于点
交于点![]() ,抛物线
,抛物线![]() 在点
在点![]() 处的切线为
处的切线为![]() ,记直线
,记直线![]() ,
, ![]() 与
与![]() 轴围成的三角形面积为
轴围成的三角形面积为![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】据报道,全国很多省市将英语考试作为高考改革的重点,一时间“英语考试该如何改革”引起广泛关注,为了解某地区学生和包括老师、家长在内的社会人士对高考英语改革的看法,某媒体在该地区选择了3 000人进行调查,就“是否取消英语听力”问题进行了问卷调查统计,结果如下表:
态度 | |||
调查人群 | 应该取消 | 应该保留 | 无所谓 |
在校学生 | 2100人 | 120人 | y人 |
社会人士 | 500人 | x人 | z人 |
已知在全体样本中随机抽取1人,抽到持“应该保留”态度的人的概率为0.06.
(1)现用分层抽样的方法在所有参与调查的人中抽取300人进行问卷访谈,问应在持“无所谓”态度的人中抽取多少人?
(2)在持“应该保留”态度的人中,用分层抽样的方法抽取6人,然后从这6人中随机抽取2人,求这2人中恰好有1个人为在校学生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知正实数列a1,a2,…满足对于每个正整数k,均有![]() ,证明:
,证明:
(Ⅰ)a1+a2≥2;
(Ⅱ)对于每个正整数n≥2,均有a1+a2+…+an≥n.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 过点
过点![]() ,其参数方程为
,其参数方程为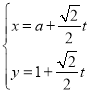 (
(![]() 为参数,
为参数,![]() ).以
).以![]() 为极点,
为极点,![]() 轴非负半轴为极轴,建立极坐标系,曲线
轴非负半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)已知曲线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,且
两点,且![]() ,求实数
,求实数![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P-ABCD中,底面ABCD是边长为3的菱形,∠ABC=60°.PA⊥面ABCD,且PA=3.F在棱PA上,且AF=1,E在棱PD上.
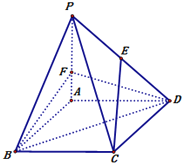
(Ⅰ)若CE∥面BDF,求PE:ED的值;
(Ⅱ)求二面角B-DF-A的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,几何体AMDCNB是由两个完全相同的四棱锥构成的几何体,这两个四棱锥的底面ABCD为正方形,![]() ,平面
,平面![]() 平面ABCD.
平面ABCD.

(1)证明:平面![]() 平面MDC.
平面MDC.
(2)若![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com