
【题目】德国著名数学家狄利克雷在数学领域成就显著,以其名命名的函数f(x)= ![]() ,称为狄利克雷函数,则关于函数f(x)有以下四个命题: ①f(f(x))=1;
,称为狄利克雷函数,则关于函数f(x)有以下四个命题: ①f(f(x))=1;
②函数f(x)是偶函数;
③任意一个非零有理数T,f(x+T)=f(x)对任意x∈R恒成立;
④存在三个点A(x1 , f(x1)),B(x2 , f(x2)),C(x3 , f(x3)),使得△ABC为等边三角形.
其中真命题的个数是( )
A.4
B.3
C.2
D.1
【答案】A
【解析】解:①∵当x为有理数时,f(x)=1;当x为无理数时,f(x)=0, ∴当x为有理数时,ff((x))=f(1)=1;当x为无理数时,f(f(x))=f(0)=1,
即不管x是有理数还是无理数,均有f(f(x))=1,故①正确;
②∵有理数的相反数还是有理数,无理数的相反数还是无理数,
∴对任意x∈R,都有f(﹣x)=f(x),故②正确;
③若x是有理数,则x+T也是有理数; 若x是无理数,则x+T也是无理数,
∴根据函数的表达式,任取一个不为零的有理数T,f(x+T)=f(x)对x∈R恒成立,故③正确;
④取x1=﹣ ![]() ,x2=0,x3=
,x2=0,x3= ![]() ,可得f(x1)=0,f(x2)=1,f(x3)=0,
,可得f(x1)=0,f(x2)=1,f(x3)=0,
∴A( ![]() ,0),B(0,1),C(﹣
,0),B(0,1),C(﹣ ![]() ,0),恰好△ABC为等边三角形,故④正确.
,0),恰好△ABC为等边三角形,故④正确.
即真命题的个数是4个,
故选:A.
【考点精析】解答此题的关键在于理解命题的真假判断与应用的相关知识,掌握两个命题互为逆否命题,它们有相同的真假性;两个命题为互逆命题或互否命题,它们的真假性没有关系.


科目:高中数学 来源: 题型:
【题目】已知函数f(x)=sin(2x+ ![]() ),f′(x)是f(x)的导函数,则函数y=2f(x)+f′(x)的一个单调递减区间是( )
),f′(x)是f(x)的导函数,则函数y=2f(x)+f′(x)的一个单调递减区间是( )
A.[ ![]() ,
, ![]() ]
]
B.[﹣ ![]() ,
, ![]() ]
]
C.[﹣ ![]() ,
, ![]() ]
]
D.[﹣ ![]() ,
, ![]() ]
]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设双曲线C:![]() (a>0,b>0)的左、右焦点分别为F1,F2,|F1F2|=2c,过F2作x轴的垂线与双曲线在第一象限的交点为A,已知Q
(a>0,b>0)的左、右焦点分别为F1,F2,|F1F2|=2c,过F2作x轴的垂线与双曲线在第一象限的交点为A,已知Q![]() ,|F2Q|>|F2A|,点P是双曲线C右支上的动点,且|PF1|+|AQ|>
,|F2Q|>|F2A|,点P是双曲线C右支上的动点,且|PF1|+|AQ|>![]() |F1F2|恒成立,则双曲线的离心率的取值范围是( )
|F1F2|恒成立,则双曲线的离心率的取值范围是( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知中心在原点的双曲线![]() 的右焦点为
的右焦点为![]() ,右顶点为
,右顶点为![]() .
.
(1)求双曲线![]() 的方程;
的方程;
(2)若直线![]() 与双曲线
与双曲线![]() 恒有两个不同的交点
恒有两个不同的交点![]() 和
和![]() ,且
,且![]() (其中
(其中![]() 为坐标原点),求实数
为坐标原点),求实数![]() 取值范围.
取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列有关命题的说法正确的是( )
A.命题“若xy=0,则x=0”的否命题为:“若xy=0,则x≠0”
B.“若x+y=0,则x,y互为相反数”的逆命题为真命题
C.命题“x∈R,使得2x2﹣1<0”的否定是:“x∈R,均有2x2﹣1<0”
D.命题“若cosx=cosy,则x=y”的逆否命题为真命题
查看答案和解析>>
科目:高中数学 来源: 题型:
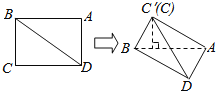
【题目】如图所示,在矩形ABCD中,![]() ,
,![]() 沿对角线将
沿对角线将![]() 折起,使点C移到
折起,使点C移到![]() 点,且C点在平面ABD的射影O恰在AB上.
点,且C点在平面ABD的射影O恰在AB上.
(1)求证:![]() 平面ACD;
平面ACD;
![]() 求直线AB与平面
求直线AB与平面![]() D所成角的正弦值.
D所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司制定了一个激励销售人员的奖励方案:当销售利润不超过15万元时,按销售利润的![]() 进行奖励;当销售利润超过15万元时,若超过部分为A万元,则超出部分按
进行奖励;当销售利润超过15万元时,若超过部分为A万元,则超出部分按![]() 进行奖励,没超出部分仍按销售利润的
进行奖励,没超出部分仍按销售利润的![]() 进行奖励
进行奖励![]() 记奖金总额为
记奖金总额为![]() 单位:万元
单位:万元![]() ,销售利润为
,销售利润为![]() 单位:万元
单位:万元![]() .
.
![]() 1
1![]() 写出该公司激励销售人员的奖励方案的函数表达式;
写出该公司激励销售人员的奖励方案的函数表达式;
![]() 2
2![]() 如果业务员老张获得
如果业务员老张获得![]() 万元的奖金,那么他的销售利润是多少万元?
万元的奖金,那么他的销售利润是多少万元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分13分)
已知圆满足:
① 截y轴所得弦长为2;
②被x轴分成两段圆弧,其弧长的比为3:1;
③圆心到直线l:x-2y=0的距离为![]() ,求该圆的方程.
,求该圆的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随机抽取某中学甲、乙两班各10名同学,测量他们的身高(单位:cm),获得身高数据的茎叶图如图7.

(1)根据茎叶图判断哪个班的平均身高较高;
(2)计算甲班的样本方差;
(3)现从乙班这10名同学中随机抽取两名身高不低于173cm的同学,求身高为176cm的同学被抽中的概率。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com