练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】A袋中有1个红球和1个黑球，B袋中有2个红球和1个黑球，A袋中任取1个球与B袋中任取1个球互换，这样的互换进行了一次，求：

    (1)A袋中红球恰是1个的概率；

    (2)A袋中红球至少是1个的概率．

    【答案】（1）；（2）

    【解析】

    将A袋中的1个红球和1个黑球分别编号为红1，黑1，B袋中的2个红球和1个黑球分别编号为红2，红3，黑2，列出基本事件空间，以及A袋中红球恰是1个得事件和)A袋中红球至少是1个的事件，利用古典概型求出各自概率.

    将A袋中的1个红球和1个黑球分别编号为红1，黑1，B袋中的2个红球和1个黑球分别编号为红2，红3，黑2，则A袋中任取1个球与B袋中任取1个球的基本事件空间为{(红1，红2)，(红1，红3)，(红1，黑2)，(黑1，红2)，(黑1，红3)，(黑1，黑2)}，由6个基本事件组成．

    (1)互换后A袋中红球恰是1个的概率P1＝＝.

    (2)互换后A袋中红球至少是1个的概率P2＝.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知某书店共有韩寒的图书6种，其中价格为25元的有2种，18元的有3种，16元的有1种．书店若把这6种韩寒的图书打包出售，据统计每套的售价与每天的销售数量如下表所示：

    售价x/元

    105

    108

    110

    112

    销售数量y/套

    40

    30

    25

    15

    (1)根据上表，利用最小二乘法得到回归直线方程，求；

    (2)若售价为100元，则每天销售的套数约为多少(结果保留到整数)?

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】为了解篮球爱好者小张的投篮命中率与打篮球时间之间的关系，下表记录了小张某月1号到5号每天打篮球时间(单位：小时)与当天投篮命中率之间的关系：

    时间

    1

    2

    3

    4

    5

    命中率

    0.4

    0.5

    0.6

    0.6

    0.4


    （1）求小张这天的平均投篮命中率；

    （2）利用所给数据求小张每天打篮球时间(单位：小时)与当天投篮命中率之间的线性回归方程；（参考公式：）

    （3）用线性回归分析的方法，预测小李该月号打小时篮球的投篮命中率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】2017年10月18日至24日，中国共产党第十九次全国人民代表大会在北京顺利召开．大会期间，北京某高中举办了一次“喜迎十九大”的读书读报知识竞赛，参赛选手为从高一年级和高二年级随机抽取的各100名学生．图1和图2分别是高一年级和高二年级参赛选手成绩的频率分布直方图．

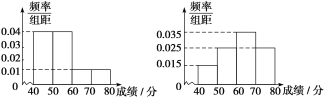
    (1)分别计算参加这次知识竞赛的两个年级学生的平均成绩；

    (2)若称成绩在68分以上的学生知识渊博，试以上述数据估计该高一、高二两个年级学生的知识渊博率；

    (3)完成下面2×2列联表，并回答能否在犯错误的概率不超过0.010的前提下，认为高一、高二两个年级学生这次读书读报知识竞赛的成绩有差异．

    分类

    成绩低于60分人数

    成绩不低于60分人数

    总计

    高一年级

    高二年级

    总计

    附：

    P(K2≥k)

    0.100

    0.050

    0.025

    0.010

    0.001

    k

    2.706

    3.841

    5.024

    6.635

    10.828

    K2＝.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】现有7名数理化成绩优秀者，其中A1，A2，A3数学成绩优秀，B1，B2物理成绩优秀，C1，C2化学成绩优秀，从中选出数学、物理、化学成绩优秀者各1名，组成一个小组代表学校参加竞赛．

    (1)求C1被选中的概率；

    (2)求A1，B1不全被选中的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某高中社团进行社会实践，对岁的人群随机抽取n人进行了一次是否开通“微博”的调查，若开通“微博”的称为“时尚族”，否则称为“非时尚族”，通过调查分别得到如图所示统计表和各年龄段人数频率分布直方图：

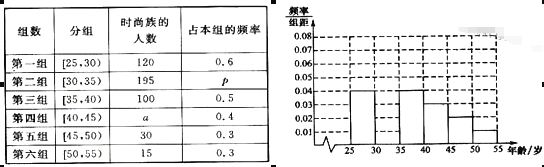
    完成以下问题：

    （Ⅰ）补全频率分布直方图并求的值；

    （Ⅱ）从岁年龄段的“时尚族”中采用分层抽样法抽取人参加网络时尚达人大赛，其中选取人作为领队，记选取的名领队中年龄在岁的人数为，求的分布列

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，点C在以AB为直径的圆O上，PA垂直于圆O所在的平面，G为△AOC的重心．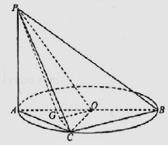
    （1）求证：平面OPG⊥平面PAC；
    （2）若PA=AB=2AC=2，求二面角A﹣OP﹣G的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆 的离心率为 ，左右焦点分别为F1 ， F2 ， 以椭圆短轴为直径的圆与直线 相切．
    （Ⅰ）求椭圆E的方程；
    （Ⅱ）过点F1、斜率为k1的直线l1与椭圆E交于A，B两点，过点F2、斜率为k2的直线l2与椭圆E交于C，D两点，且直线l1 ， l2相交于点P，若直线OA，OB，OC，OD的斜率kOA ， kOB ， kOC ， kOD满足kOA+kOB=kOC+kOD ， 求证：动点P在定椭圆上，并求出此椭圆方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某大学为调查来自南方和北方的同龄大学生的身高差异，从2016级的年龄在18～19岁之间的大学生中随机抽取了来自南方和北方的大学生各10名，测量他们的身高，量出的身高如下(单位：cm)：

    南方：158，170，166，169，180，175，171，176，162，163.

    北方：183，173，169，163，179，171，157，175，184，166.

    (1)根据抽测结果，画出茎叶图，对来自南方和北方的大学生的身高作比较，写出统计结论．

    (2)设抽测的10名南方大学生的平均身高为x cm，将10名南方大学生的身高依次输入如图所示的程序框图进行运算，问输出的s大小为多少？并说明s的统计学意义．

    (3)为进一步调查身高与生活习惯的关系，现从来自南方的这10名大学生中随机抽取2名身高不低于170 cm的学生，求身高为176 cm的学生被抽中的概率．

    查看答案和解析>>

    同步练习册答案