
【题目】从某山区养殖场散养的3500头猪中随机抽取5头,测量猪的体长x(cm)和体重y(kg),得如下测量数据:
猪编号 | 1 | 2 | 3 | 4 | 5 |
x | 169 | 181 | 166 | 185 | 180 |
y | 95 | 100 | 97 | 103 | 101 |
(1)当且仅当x,y满足:x≥180且y≥100时,该猪为优等品,用上述样本数据估计山区养殖场散养的3500头猪中优等品的数量;
(2)从抽取的上述5头猪中,随机抽取2头中优等品数x的分布列及其数学期望.
【答案】
(1)解:由已知随机抽取的5头猪中,优等品有3头,
∴估计山区养殖场散养的3500头猪中优等品的数量为:
3500× ![]() =2100(头)
=2100(头)
(2)解:∵抽取的5头猪中,优等品有3头,非优等品有2头,
∴随机抽取2头中优等品数X的可能取值为0,1,2,
P(X=0)= ![]() =
= ![]() ,
,
P(X=1)= ![]() =
= ![]() ,
,
P(X=2)= ![]() =
= ![]() ,
,
∴X的分布列为:
X | 0 | 1 | 2 |
P |
|
|
|
EX= ![]() =
= ![]()
【解析】(1)由已知随机抽取的5头猪中,优等品有3头,由此能估计山区养殖场散养的3500头猪中优等品的数量.(2)抽取的5头猪中,优等品有3头,非优等品有2头,随机抽取2头中优等品数X的可能取值为0,1,2,分别求出相应的概率,由此能求出X的分布列和EX.
【考点精析】解答此题的关键在于理解离散型随机变量及其分布列的相关知识,掌握在射击、产品检验等例子中,对于随机变量X可能取的值,我们可以按一定次序一一列出,这样的随机变量叫做离散型随机变量.离散型随机变量的分布列:一般的,设离散型随机变量X可能取的值为x1,x2,.....,xi,......,xn,X取每一个值 xi(i=1,2,......)的概率P(ξ=xi)=Pi,则称表为离散型随机变量X 的概率分布,简称分布列.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】连续抛掷同一颗均匀的骰子,令第i次得到的点数为ai , 若存在正整数k,使a1+a2+…+ak=6,则称k为你的幸运数字.
(1)求你的幸运数字为3的概率;
(2)若k=1,则你的得分为5分;若k=2,则你的得分为3分;若k=3,则你的得分为1分;若抛掷三次还没找到你的幸运数字则记0分,求得分X的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数 ![]() .
.
(1)用含a的式子表示b;
(2)令F(x)= ![]() ,其图象上任意一点P(x0 , y0)处切线的斜率
,其图象上任意一点P(x0 , y0)处切线的斜率 ![]() 恒成立,求实数a的取值范围;
恒成立,求实数a的取值范围;
(3)若a=2,试求f(x)在区间 ![]() 上的最大值.
上的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,CA,CB分别与圆O切于A,B两点,AE是直径,OF平分∠BOE交CB的延长线于F,BD∥AC. 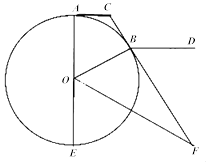
(1)证明:OB2=BCBF;
(2)证明:∠DBF=∠AOB.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】抛物线![]() 的焦点为
的焦点为![]() 上任一点
上任一点![]() 在
在![]() 轴上的射影为
轴上的射影为![]() 中点为
中点为![]() ,
,![]() .
.
(1)求动点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)直线![]() 过
过![]() 与
与![]() 从下到上依次交于
从下到上依次交于![]() ,与
,与![]() 交于
交于![]() ,直线
,直线![]() 过
过![]() 与
与![]() 从下到上依次交于
从下到上依次交于![]() ,与
,与![]() 交于
交于![]() ,
,![]() ,
,![]() 的斜率之积为
的斜率之积为![]() ,设
,设![]() 的面积分别为
的面积分别为![]() ,是否存在
,是否存在![]() 使得
使得![]() 成等比数列?若存在,求
成等比数列?若存在,求![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 、
、![]() 分别是椭圆
分别是椭圆![]() 的左、右焦点.
的左、右焦点.
(1)若![]() 是该椭圆上的一个动点,求
是该椭圆上的一个动点,求![]() 的最大值和最小值;
的最大值和最小值;
(2)设过定点![]() 的直线与椭圆交于不同的两点
的直线与椭圆交于不同的两点![]() 、
、![]() ,且
,且![]() 为锐角(其中
为锐角(其中![]() 为坐标原点),求直线
为坐标原点),求直线![]() 的斜率
的斜率![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线C1:x2=y,圆C2:x2+(y﹣4)2=1的圆心为点M
(1)求点M到抛物线C1的准线的距离;
(2)已知点P是抛物线C1上一点(异于原点),过点P作圆C2的两条切线,交抛物线C1于A,B两点,若过M,P两点的直线l垂直于AB,求直线l的方程.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com