
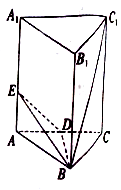
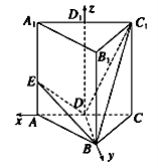
【题目】已知正三棱柱![]() 中,
中,![]() ,
,![]() ,点
,点![]() 为
为![]() 的中点,点
的中点,点![]() 在线段
在线段![]() 上.
上.
(1)当![]() 时,求证:
时,求证:![]() ;
;
(2)是否存在点![]() ,使二面角
,使二面角![]() 等于
等于![]() ?若存在,求
?若存在,求![]() 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
【答案】(1)证明见解析;(2)存在点![]() ,且
,且![]() .
.
【解析】
试题分析:(1)借助题设条件运用线面垂直的性质定理推证;(2)借助题设运用空间向量的数量积公式建立方程求解.
试题解析:
(1)证明:连接![]() ,
,
因为![]() 为正三棱柱,所以
为正三棱柱,所以![]() 为正三角形,
为正三角形,
又因为![]() 为
为![]() 的中点,所以
的中点,所以![]() ,
,
又平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() ,所以
,所以![]() .
.
因为![]() ,
,![]() ,
,![]() ,所以
,所以![]() ,
,![]() ,
,
所以在![]() 中,
中,![]() ,
,
在![]() 中,
中,![]() ,所以
,所以![]() ,即
,即![]() ,
,
又![]() ,
,
所以![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() .
.
(2)假设存在点![]() 满足条件,设
满足条件,设![]() ,
,
取![]() 的中点
的中点![]()
![]() ,连接
,连接![]() ,则
,则![]() 平面
平面![]() ,
,
所以![]() ,
,![]() ,
,
分别以![]() ,
,![]() ,
,![]() 所在直线为
所在直线为![]() ,
,![]() ,
,![]() 轴建立空间直角坐标系
轴建立空间直角坐标系![]() ,
,
则![]() ,
,![]() ,
,![]() ,
,
所以![]() ,
,![]() ,
,![]() ,
,![]() ,
,
设平面![]() 的一个法向量为
的一个法向量为![]() ,
,
则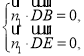 即
即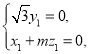 令
令![]() ,得
,得![]() ,
,
同理,平面![]() 的一个法向量为
的一个法向量为![]() ,
,
则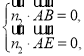 即
即 取
取![]() ,得
,得![]() ,
,
所以![]() ,解得
,解得![]() ,
,
故存在点![]() ,当
,当![]() 时,二面角
时,二面角![]() 等于
等于![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】某商品每件成本5元,售价14元,每星期卖出75件.如果降低价格,销售量可以增加,且每星期多卖出的商品件数![]() 与商品单价的降低值
与商品单价的降低值![]() (单位:元,
(单位:元,![]() )的平方成正比,已知商品单价降低1元时,一星期多卖出5件.
)的平方成正比,已知商品单价降低1元时,一星期多卖出5件.
(1)将一星期的商品销售利润![]() 表示成
表示成![]() 的函数;
的函数;
(2)如何定价才能使一个星期的商品销售利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,在高为2的梯形![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,过
,过![]() 、
、![]() 分别作
分别作![]() ,
, ![]() ,垂足分别为
,垂足分别为![]() 、
、![]() 。已知
。已知![]() ,将梯形
,将梯形![]() 沿
沿![]() 、
、![]() 同侧折起,得空间几何体
同侧折起,得空间几何体![]() ,如图2。
,如图2。
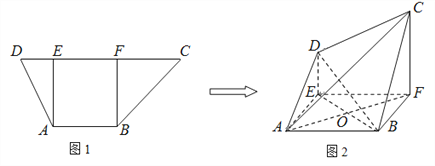
(1)若![]() ,证明:
,证明: ![]() ;
;
(2)若![]() ,证明:
,证明: ![]() ;
;
(3)在(1),(2)的条件下,求三棱锥![]() 的体积。
的体积。
查看答案和解析>>
科目:高中数学 来源: 题型:
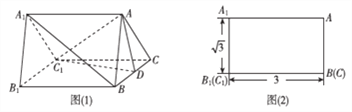
【题目】如图(1)是一个水平放置的正三棱柱![]() ,
, ![]() 是棱
是棱![]() 的中点,正三棱柱的主视图如图(2).
的中点,正三棱柱的主视图如图(2).
(1)图(1)中垂直于平面![]() 的平面有哪几个(直接写出符合要求的平面即可,不必说明或证明)
的平面有哪几个(直接写出符合要求的平面即可,不必说明或证明)
(2)求正三棱柱![]() 的体积;
的体积;
(3)证明: ![]() 平面
平面![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() (
(![]() ,
,![]() ,
,![]() ,
,![]() )的图象在点
)的图象在点![]() 处的切线的斜率为
处的切线的斜率为![]() ,且函数
,且函数![]() 为偶函数.若函数
为偶函数.若函数![]() 满足下列条件:①
满足下列条件:①![]() ;②对一切实数
;②对一切实数![]() ,不等式
,不等式![]() 恒成立.
恒成立.
(1)求函数![]() 的表达式;
的表达式;
(2)设函数![]() (
(![]() )的两个极值点
)的两个极值点![]() ,
,![]() (
(![]() )恰为
)恰为![]() 的零点.当
的零点.当![]() 时,求
时,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2016年12月16日,科幻片《侠盗一号》上映,上映至今,全球累计票房高达8亿美金.为了了解娄底观众的满意度,某影院随机调查了本市观看影片的观众,并用“10分制”对满意度进行评分,分数越高满意度越高,若分数不低于9分,则称该观众为“满意观众”.现从调查人群中随机抽取12名.如图所示的茎叶图记录了他们的满意度分数(以小数点前的一位数字为茎,小数点后的一位数字为叶).
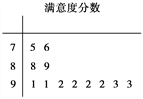
(1)求从这12人中随机选取1人,该人不是“满意观众”的概率;
(2)从本次所记录的满意度评分大于9.1的“满意观众”中随机抽取2人,求这2人得分不同的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
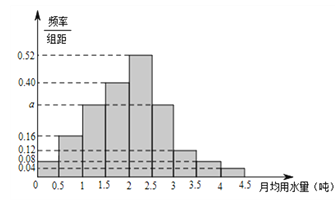
【题目】水是万物之本、生命之源,节约用水,从我做起.我国是世界上严重缺水的国家,某市政府为了鼓励居民节约用水,计划调整居民生活用水收费方案,拟确定一个合理的月用水量标准![]() (吨)、一位居民的月用水量不超过
(吨)、一位居民的月用水量不超过![]() 的部分按平价收费,超出
的部分按平价收费,超出![]() 的部分按议价收费.为了了解居民用水情况,通过抽样,获得了某年100位居民每人的月均用水量(单位:吨),将数据按照[0,0.5),[0.5,1),…,[4,4.5)分成9组,制成了如图所示的频率分布直方图.(1)求直方图中a的值;(2)设该市有30万居民,估计全市居民中月均用水量不低于3吨的人数,并说明理由;(3)若该市政府希望使85%的居民每月的用水量不超过标准
的部分按议价收费.为了了解居民用水情况,通过抽样,获得了某年100位居民每人的月均用水量(单位:吨),将数据按照[0,0.5),[0.5,1),…,[4,4.5)分成9组,制成了如图所示的频率分布直方图.(1)求直方图中a的值;(2)设该市有30万居民,估计全市居民中月均用水量不低于3吨的人数,并说明理由;(3)若该市政府希望使85%的居民每月的用水量不超过标准![]() (吨),估计
(吨),估计![]() 的值,并说明理由.
的值,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了完成对某城市的工薪阶层是否赞成调整个人所得税税率的调查,随机抽取了60人,作出了他们的月收入频率分布直方图(如图),同时得到了他们月收入情况与赞成人数统计表(如下表):
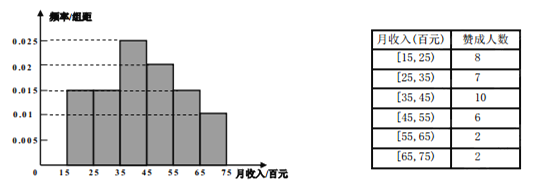
(1)试根据频率分布直方图估计这60人的平均月收入;
(2)若从月收入(单位:百元)在[65,75)的被调查者中随机选取2人进行追踪调查,求2人都不赞成的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com