
【题目】“龟兔赛跑”讲述了这样的故事:领先的兔子看着慢慢爬行的乌龟,骄傲起来,睡了一觉,当它醒来时,发现乌龟快到终点了,于是急忙追赶,但为时已晚,乌龟还是先到达了终点.用![]() ,
,![]() 分别表示乌龟和兔子所行的路程,
分别表示乌龟和兔子所行的路程,![]() 为时间,则与故事情节相吻合的是( )
为时间,则与故事情节相吻合的是( )
A.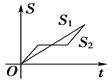 B.
B.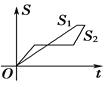 C.
C.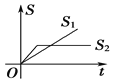 D.
D.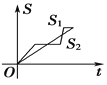
科目:高中数学 来源: 题型:
【题目】已知椭圆M:: ![]() (a>0)的一个焦点为F(﹣1,0),左右顶点分别为A,B.经过点F的直线l与椭圆M交于C,D两点.
(a>0)的一个焦点为F(﹣1,0),左右顶点分别为A,B.经过点F的直线l与椭圆M交于C,D两点.
(1)求椭圆方程;
(2)当直线l的倾斜角为45°时,求线段CD的长;
(3)记△ABD与△ABC的面积分别为S1和S2 , 求|S1﹣S2|的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,DOAB是边长为2的正三角形,当一条垂直于底边OA(垂足不与O,A重合)的直线x=t从左至右移动时,直线l把三角形分成两部分,记直线l左边部分的面积y.

(Ⅰ)写出函数y= f(t)的解析式;
(Ⅱ)写出函数y= f(t)的定义域和值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数![]() 满足如下四个条件:
满足如下四个条件:
①定义域为![]() ;
;
②![]() ;
;
③当![]() 时,
时,![]() ;
;
④对任意![]() 满足
满足![]() .
.
根据上述条件,求解下列问题:
⑴求![]() 及
及![]() 的值.
的值.
⑵应用函数单调性的定义判断并证明![]() 的单调性.
的单调性.
⑶求不等式![]() 的解集.
的解集.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知各项都是正数的数列{an}的前n项和为Sn , Sn=an2+ ![]() an , n∈N*
an , n∈N*
(1)求数列{an}的通项公式;
(2)设数列{bn}满足:b1=1,bn﹣bn﹣1=2an(n≥2),求数列{ ![]() }的前n项和Tn
}的前n项和Tn
(3)若Tn≤λ(n+4)对任意n∈N*恒成立,求λ的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,点列{An}、{Bn}分别在锐角两边(不在锐角顶点),且|AnAn+1|=|An+1An+2|,An≠An+2 , |BnBn+1|=|Bn+1Bn+2|,Bn≠Bn+1 , n∈N*(P≠Q表示点P与Q不重合),若dn=|AnBn|,Sn为△AnBnBn+1的面积,则( ) 
A.{dn}是等差数列
B.{Sn}是等差数列
C.{d ![]() }是等差数列
}是等差数列
D.{S ![]() }是等差数列
}是等差数列
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将函数f(x)= ![]() sin2x﹣
sin2x﹣ ![]() cos2x+1的图象向左平移
cos2x+1的图象向左平移 ![]() 个单位,再向下平移1个单位,得到函数y=g(x)的图象,则下列关予函数y=g(x)的说法错误的是( )
个单位,再向下平移1个单位,得到函数y=g(x)的图象,则下列关予函数y=g(x)的说法错误的是( )
A.函数y=g(x)的最小正周期为π
B.函数y=g(x)的图象的一条对称轴为直线x= ![]()
C.![]() g(x)dx=
g(x)dx= ![]()
D.函数y=g(x)在区间[ ![]() ,
, ![]() ]上单调递减
]上单调递减
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com