练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    “ab≠0”是指．


    1. A.
      a≠0且b≠0
    2. B.
      a≠0或b≠0
    3. C.
      a、b中至少有一个不为0
    4. D.
      a、b不同时为0
    A
    ab≠0是指a≠0且b≠0，所以选A．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    已知函数f（x）=mx3+nx2（m、n∈R，m≠0）的图象在（2，f（2））处的切线与x轴平行．
    （1）求n，m的关系式并求f（x）的单调减区间；
    （2）证明：对任意实数0＜x1＜x2＜1，关于x的方程：f′(x)-
    f(x2)-f(x1)
    x2-x1
    =0    在（x1，x2）恒有实数解
    （3）结合（2）的结论，其实我们有拉格朗日中值定理：若函数f（x）是在闭区间[a，b]上连续不断的函数，且在区间（a，b）内导数都存在，则在（a，b）内至少存在一点x0，使得f′(x0)=
    f(b)-f(a)
    b-a
    ．如我们所学过的指、对数函数，正、余弦函数等都符合拉格朗日中值定理条件．试用拉格朗日中值定理证明：
    当0＜a＜b时，
    b-a
    b
    ＜ln
    b
    a
    ＜
    b-a
    a
    （可不用证明函数的连续性和可导性）．

    查看答案和解析>>

    科目：高中数学 来源：新课程高中数学疑难全解 题型：013

    “ab≠0”是指(　　)．

    [　　]

    A．a≠0且b≠0

    B．a≠0或b≠0

    C．a、b中至少有一个不为0

    D．a、b不同时为0

    查看答案和解析>>

    科目：高中数学 来源：上海市十三校2012届高三第二次联考数学文科试题 题型：044

    现代城市大多是棋盘式布局(如北京道路几乎都是东西和南北走向)．在这样的城市中，我们说的两点间的距离往往不是指两点间的直线距离(位移)，而是实际路程(如图)．在直角坐标平面内，我们定义A(x1，y1)，B(x2，y2)两点间的“直角距离”为：D(AB)＝|x1－x2|＋|y1－y2|．

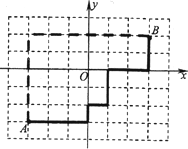
    (1)已知A(－3，－3)，B(3，2)，求A、B两点的距离D(AB)．

    (2)求到定点M(1，2)的“直角距离”为2的点的轨迹方程．

    并写出所有满足条件的“格点”的坐标(格点是指横、纵坐标均为整数的点)．

    (3)求到两定点F1、F2的“直角距离”和为定值2a(a＞0)的动点轨迹方程，并在直角坐标系内作出该动点的轨迹．

    ①F1(－1，0)，F2(1，0)，a＝2；

    ②F1(－1，－1)，F2(1，1)，a＝2；

    ③F1(－1，－1)，F2(1，1)，a＝4．

    查看答案和解析>>

    科目：高中数学 来源：上海市十三校2012届高三第二次联考数学理科试题 题型：044

    现代城市大多是棋盘式布局(如北京道路几乎都是东西和南北走向)．在这样的城市中，我们说的两点间的距离往往不是指两点间的直线距离(位移)，而是实际路程(如图)．在直角坐标平面内，我们定义A(x1，y1)，B(x2，y2)两点间的“直角距离”为：D(AB)＝|x1－x2|＋|y1－y2|．

    (1)在平面直角坐标系中，写出所有满足到原点的“直角距离”为2的“格点”的坐标．(格点指横、纵坐标均为整数的点)

    (2)求到两定点F1、F2的“直角距离”和为定值2a(a＞0)的动点轨迹方程，并在直角坐标系内作出该动点的轨迹．

    ①F1(－1，0)，F2(1，0)，a＝2；

    ②F1(－1，－1)，F2(1，1)，a＝2；

    ③F1(－1，－1)，F2(1，1)，a＝4．

    (3)写出同时满足以下两个条件的“格点”的坐标，并说明理由(格点指横、纵坐标均为整数的点)．

    ①到A(－1，－1)，B(1，1)两点“直角距离”相等；

    ②到C(－2，－2)，D(2，2)两点“直角距离”和最小．

    查看答案和解析>>

    同步练习册答案