
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 ①,命题“?x∈R,x2+x+1>0”的否定是:“?x0∈R,x02+x0+1≤0”;
②,命题“若x=y,则sinx=siny”的否命题是:“若x≠y,则sinx≠siny”;
③,当“7<k<9”时,满足k-4>10-k>0,此时“方程$\frac{{x}^{2}}{k-4}$+$\frac{{y}^{2}}{10-k}$=1表示焦点在x轴上的椭圆“;若“方程$\frac{{x}^{2}}{k-4}$+$\frac{{y}^{2}}{10-k}$=1表示焦点在x轴上的椭圆,则k-4>10-k>0,即7<k<10;
④,m=-3时“l1:2x+(m+1)y+4=0与l2:mx+3y-2=0平行.
解答 解:对于①,命题“?x∈R,x2+x+1>0”的否定是:“?x0∈R,x02+x0+1≤0”,故正确;
对于②,命题“若x=y,则sinx=siny”的否命题是:“若x≠y,则sinx≠siny”,故错;
对于③,当“7<k<9”时,满足k-4>10-k>0,此时“方程$\frac{{x}^{2}}{k-4}$+$\frac{{y}^{2}}{10-k}$=1表示焦点在x轴上的椭圆“;若“方程$\frac{{x}^{2}}{k-4}$+$\frac{{y}^{2}}{10-k}$=1表示焦点在x轴上的椭圆,则k-4>10-k>0,即7<k<10,故正确;
对于④,“m=-3”时“l1:2x+(m+1)y+4=0与l2:mx+3y-2=0平行”,故错.
故选:B.
点评 本题考查了命题真假的判定,属于基础题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | 2x+y+7=0 | B. | 2x-y+5=0 | C. | x-2y+1=0 | D. | x-2y+5=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| x | 3 | 4 | 5 | 5 | 7 |
| y | 2 | 4 | 5 | 6 | 8 |
| A. | (5,5) | B. | (4.5,5) | C. | (4.8,5) | D. | (5,6) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若f(x1)=f(x2)=0,则x1-x2=kπ(k∈Z) | |
| B. | 函数f(x)的图象关于(-$\frac{π}{8}$,0)对称 | |
| C. | 函数f(x)的图象与g(x)=3cos(2x+$\frac{π}{4}$)的图象相同 | |
| D. | 函数f(x)在[-$\frac{1}{8}$π,$\frac{3}{8}$π]上递增 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2x-3y+4=0 | B. | 3x-2y+1=0 | C. | 2x+3y-8=0 | D. | 3x+2y-7=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
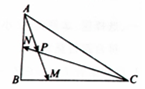 在△ABC中,$\overrightarrow{AM}$=$\frac{3}{4}$$\overrightarrow{AB}$+$\frac{1}{4}$$\overrightarrow{AC}$
在△ABC中,$\overrightarrow{AM}$=$\frac{3}{4}$$\overrightarrow{AB}$+$\frac{1}{4}$$\overrightarrow{AC}$查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com